J'ai un exercice en electrocinetique : dipole RLC en régime sinusoidal forcé,
il y'a deux parties, dans la 1ere il s'agit de faire une etude d'un circuit RLC série, c'est simple,
dans la 2ème, on considère le circuit: constitué de deux dipoles rLC et un condensateur de capacité C₀ , le dipole rLC etant le même que celui étudié dans la partie 1.
On établit aux bornes A et B une difference de potentiel sinusoidale: u(t)=U2 cos(t)

1- etablir un systeme de deux équations differentielles donnant l'évolution des tensions u1(t)et u2(t) .
2- En déduire en RSF un système de deux équations en U1_ et U2_ (notation complexe) et un autre système de deux équations en I1_ et I2_ avec U1_ , U2_ et I1_ I2_ définis par:
u1_(t)= U1_2 exp(jt)
u2_(t)= U2__2 exp(jt)
i1_(t)=I1___2 exp(jt)
i2_(t)=I2___2 exp(jt)

et puis d'autres questions j'essayerais de les mettre plus tard,
j'ai écris la loi des mailles et la loi des noeuds, après j'ai commencé à calculer j'avais ces équations:

1) u= r(i1+i2) + Ld(i1+i2)/dt + u1 + u2
on peut remplacer i1 par cdu1/dt et i2 par Cdu2/dt
2) i1=i2+i3 <=> cdu1/dt = cdu2/dt + u3
3) u3= ri2 + ldi2/dt + u2
j'ai refaits les calculs deux fois, j'ai des dérivées d'ordre 4 et 3,
mais uand je vérifie avec les unités je trouve que ce n'est pas homogène:
u= l²C₀C d⁴u2/dt⁴ + rLCC₀ d³u3/dt³ + d²u2/dt² ( L(C+C₀) + Lr + L²C + r² + C₀L) + du2/dt ( r(C+C₀) + rC + r/C ) + u2( ((C+C₀)/C) + 1)

je sais pas si le fait d'intègrer me facilitera les calculs, mais je pense que c'est la même chose,
pour la 2ème, on passera à la notation complexe,
Merci d'avance.
voilà le circuit: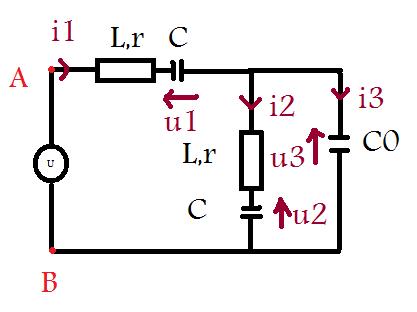

_{* Tom_Pascal > image placée sur le serveur de l', merci d'en faire autant la prochaine fois Madi76 *}