Inscription / Connexion Nouveau Sujet
Circuit RLC
Bonjour , j?ai un petit soucis pour débuter cet exercice , le fait que le condensateur sois en parallèle avec la résistance me déstabilise un peu et je ne sais pas comment m?y prendre
Merci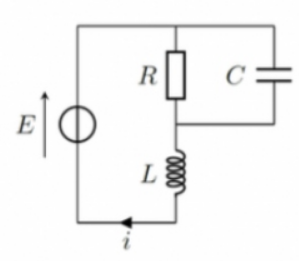
* mmalou > Image recadrée, sur la figure uniquement ! Si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum Zzzine  *
*
J'ai au début penser que le condensateur pouvait être simplifier du schéma étant donné le fait qu'il sois déchargé et que par conséquent la tension a ses bornes est donc nul mais je ne suis pas sûr
Bonsoir
Pour t'aider, il faudrait l'énoncé complet. S'agit-il d'étudier un régime transitoire ? Quel est l'état initial ?
Bonsoir
Pour t'aider, il faudrait l'énoncé complet. S'agit-il d'étudier un régime transitoire ? Quel est l'état initial ?
Bonsoir désolé voici l'énoncé :
Considérons le circuit représenté ci-contre, où le condensateur est initialement déchargé.
Le générateur fournit un échelon de tension, sa f.é.m. passant de 0 à E à l'instant t=0 .
1. Établir l'équation différentielle vérifiée par le courant .
2. L'écrire sous forme canonique en introduisant deux grandeurs et que l'on interprétera.
3. Expliquer qualitativement pourquoi il n'est pas surprenant que le facteur de qualité du circuit
s'écrive .
3. Donner la valeur du courant et de sa dérivée à l'instant initial.
5 - En supposant , donner l'expression de et tracer son allure.
C'est clair maintenant !
La tension commune aux bornes de R et de C est :
Il faut ensuite appliquer la loi des nœuds :
En remplaçant u et sa dérivée par les expressions déduites de la première relation, on obtient l'équation différentielle du second ordre vérifiée par i(t).
J'ai appliquer ce que vous m'avez conseillé et j'ai fini par trouver i = E - L di/dt + LC d2i/dt2 est-ce le bon résultat ?
Merci
est-ce le bon résultat ?
Non car ton résultat n'est pas homogène. Le terme de gauche est une intensité ; les trois termes de droite devraient tous les trois être homogène à une intensité. Relis bien mon précédent message. L'équation différentielle doit aussi faire intervenir la résistance.


