Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Circuit RLC

Posté par
fidele11 21-09-21 à 11:55

Bonjour,
J'ai besoin d'un coup de main pour un exercice.
Merci d'avance.


EXERCICE
On constitue un circuit comportant un condensateur de capacité C = 73, 4 µF en parallèle avec une bobine de
résistance R = 25 Ω et l'inductance L = 0,138 H. On établit entre ses bornes M et N la tension alternative
sinusoidale : u = 110√2sin(100πt). sachant qu'entre les intensités instantanées du courant qui traversent les
différentes branches du circuit, on a la relation : i = i1 + i2.
1. Donner les expressions des intensités instantanées i1 et i2 en fonction du temps.
2. A l'aide d'une construction de FRESNEL, déterminer l'expression de l'intensité instantanée i du courant
principal.
Calculer l'intensité éfficace.


Mon début:
1) Expressions des intensités instantanées.
Sur mon schéma, i1 est l'intensité du courant dans la branche du circuit comportant le condensateur et i2 celle de la branche comportant la bobine.
Uc et Ub sont les tensions au borne du condensateur et de la bobine.

En parallèle, U=Uc=Ub
U=Uc <=> U=q/C , q et C étant respectivement la charge et la capacité du condensateur.
<=> U*C=q . or i1=dq/dt  Donc je déduis que i1=d(U*C)/dt =CdU/dt
finalement i1(t)=11000π√2cos(100πt).

Je détermine à présent i2:
U=Ub=Ri2 + Ldi2/dt
<=> \frac{di_2}{dt}+\frac{R}{L}i_2=\frac{U}{L}
C'est une équation differentielle de premier ordre avec second membre.
Je trouve comme solution i_2(t)=Ae^{-\frac{R}{L}t}+\frac{U}{R} ... J'aimerais savoir si je peux l'écrire sous forme d'une fonction trigonométrique pour pouvoir évoluer ...

Posté par
vanoisere : Circuit RLC 21-09-21 à 18:05

Bonjour
Attention : il s'agit ici d'étudier le circuit uniquement en régime sinusoïdal établi, pas en régime transitoire.
Tu as déjà étudié l'impédance d'une bobine (r,L) en régime sinusoïdal : relation entre U (tension efficace) et I2  : intensité efficace du courant traversant la bobine.
Il te faut alors représenter les vecteurs de Fresnel associés à u(t), à i1(t) et à i2(t).
Tu peux ensuite représenter le vecteur de Fresnel associé à i(t) sachant que i(t)=i1(t)+i2(t).
Je te laisse réfléchir et proposer une solution.

Posté par
fidele11re : Circuit RLC 22-09-21 à 09:33

Bonjour,
  
L'impédence de la bobine est donnnée par U/I2 = √(R²+ (Lω)²))
De cette expression, l'intensité éfficace I2 vaut
I2=U/√(R²+(Lw)²) . En application numérique I2≈2,2 A soit l'intensité maximale I2m = 3,11 A .

i2(t)=3,11cos(100πt+φ) A avec φ à déterminer.
On avait précedemment :
i1(t)=3,59cos(100πt) A
u(t)=110√2sin(100πt) V
<=> u(t)=110√2cos(100πt-π/2) V.

Pour pouvoir representer le vecteur de Fresnel de l'intensité i2, il me faut d'abord trouver sa phase initiale φ n'est ce pas?

Posté par
vanoisere : Circuit RLC 22-09-21 à 21:33

Attention : lors de tes études précédentes, tu as montré qu'une bobine (L,r) produit une avance de phase de u(t) par rapport à i2(t) égale à . Ici, l'énoncé impose de choisir arbitrairement nulle la phase initiale de u(t). Cela signifie que i2(t) est en retard de phase de par rapport à u(t).

Posté par
fidele11re : Circuit RLC 23-09-21 à 15:40

on avait u(t)=110√2sin(100πt)   ...Donc si je comprends bien je dois conserver la fonction sinus pour u(t) pour garder sa phase initiale nulle (?)

i2(t)=3,11cos(100πt+φ) =3,11sin(100πt+π/2 + φ)
pour que la tension u soit en avance de phase il faudrait que π/2 + φ<0 ..

Posté par
vanoisere : Circuit RLC 23-09-21 à 21:51

Tu n'as pas bien compris mon message précédent... Si on choisit l'origine des temps de sorte que :

u(t)=U_{m}.\sin\left(\omega.t\right)

alors :

i_{2(t)}=I_{2m}.\sin\left(\omega.t-\varphi_{2}\right)

avec :

I_{2m}=\dfrac{U_{m}}{Z}=\dfrac{U_{m}}{\sqrt{L^{2}.\omega^{2}+r^{2}}}\quad et\quad\varphi_{2}=\arctan\left(\dfrac{L.\omega}{r}\right)

Tout cela a été étudié lors de précédents messages... Attention aux signes concernant la phase !

Posté par
fidele11re : Circuit RLC 23-09-21 à 22:57

Okay d'accord .
En application numérique I_{2m}=3,11 A.

Et \varphi_{2} ≈ 60,03° ≈ π/3 rad.

Posté par
fidele11re : Circuit RLC 23-09-21 à 22:59

1. On a finalement :
i1(t)=3,59cos(100πt) A
i2(t)=3,11cos(100πt-π/3) A

Posté par
vanoisere : Circuit RLC 24-09-21 à 23:16

D'accord pour i2(t) mais tu n'as pas tenu compte du déphasage entre u(t) et i1(t) provoqué par le condensateur.
Il faut ensuite étudier les caractéristiques du vecteur de Fresnel associé à la somme :
i(t)=i1(t)+i2(t)

Posté par
fidele11re : Circuit RLC 25-09-21 à 23:03

Le déphasage entre u(t) et i1(t) vaut φ=arctan((-1/cω)/R) ≈-60° ≈ -π/3 rad/s .
Ainsi i1(t)=3,59cos(100πt -π/3) A

Posté par
vanoisere : Circuit RLC 25-09-21 à 23:45

A ce que je comprends de l'énoncé (pas de schéma fourni), le condensateur est seul dans sa branche, cette branche étant en parallèle avec la bobine (L,R).

Posté par
fidele11re : Circuit RLC 26-09-21 à 22:53

Et donc dans ce cas, la phase initiale de i1 serait π/3 ?

Posté par
fidele11re : Circuit RLC 26-09-21 à 22:55

c'est - à -dire  i1(t)=3,59cos(100πt +π/3) A

Posté par
vanoisere : Circuit RLC 27-09-21 à 09:23

Pourquoi /3 ? Quel est le déphasage entre l'intensité du courant circulant dans la branche d'un condensateur et la tension aux bornes du condensateur  lorsque cette branche ne contient que le condensateur (pas de résistance) ?

Posté par
fidele11re : Circuit RLC 27-09-21 à 20:09

Le déphasage entre u et i pour un circuit RLC (série) est φ=arctan((Lω-1/cω)/R).

Pour une branche ne renfermant qu'un condensateur (L=0 ; R=0) ... -1/Rcw semble être infinie.
Là ça parait un peu complexe.

Posté par
vanoisere : Circuit RLC 27-09-21 à 22:53

Tu peux t'en sortir par ton raisonnement dans la mesure où :

x\rightarrow-\frac{\pi}{2}\quad si\quad\tan\left(x\right)\rightarrow-\infty

mais attention : la formule que tu utilises fournit le déphasage de u(t) par rapport à i1(t) et ici, il faut trouver le déphasage de i1(t) par rapport à u(t).

Sinon, tu obtiens simplement la démonstration du résultat à partir des valeurs instantanées :

u_{(t)}=U.\sqrt{2}.\sin\left(\omega.t\right)

i_{1(t)}=C\frac{du(t)}{dt}=C.\omega.U.\sqrt{2}.\cos\left(\omega.t\right)=C.\omega.U.\sqrt{2}.\sin\left(\omega.t+\frac{\pi}{2}\right)

Posté par
fidele11re : Circuit RLC 28-09-21 à 08:31

D'accord, merci je vois maintenant .

i1(t)=3,59sin(100πt+π/2) A
i2(t)=3,11cos(100πt-π/3) A

Pour la suite, je dois déterminer l'intensité instantanée du courant principal i(t)=i1(t) + i2(t) :
i(t)=3,59sin(100πt+π/2) + 3,11cos(100πt-π/3)

Posté par
vanoisere : Circuit RLC 28-09-21 à 10:31

C'est bien cela !

Posté par
fidele11re : Circuit RLC 28-09-21 à 21:46

Pour construire, les vecteurs de Fresnel il me faut d'abord utiliser une même fonction trigonométrique pour faciliter la tâche.
i1(t)=3,59cos(wt) A et i2(t)=3,11cos(wt-π/3) A .

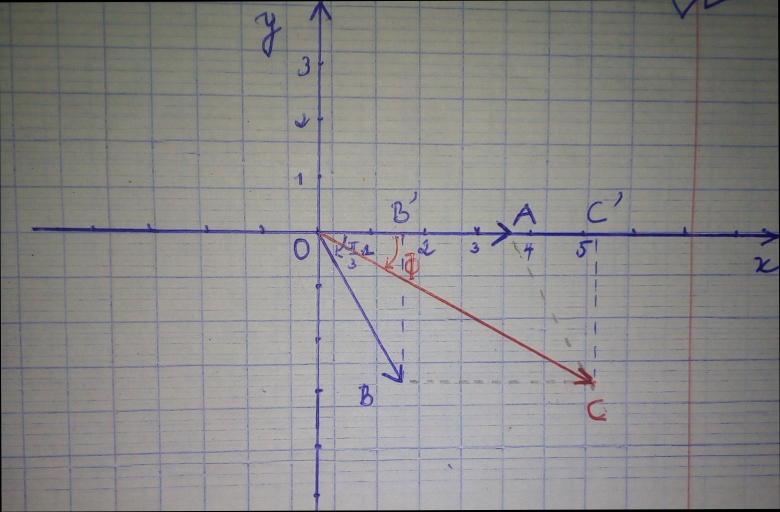
J'ai pris comme unité graphique 1cm.
O est l'orignine du repère choisi.
Je désigne par \vec{OA} le vecteur associé à i1 et par \vec{OB} celui associé à i2.
\vec{OC} est la somme des vecteurs associés à i1 et à i2.

L'expression de i est :
i(t)=Im*cos(wt+Φ) A.
Im est égale à la norme du vecteur associé à i(t) : Im=OC.

Φ est l'angle entre l'origine des phases et le vecteur \vec{OC}.

*Calcul de OC :
OC²=OA²+OB²+2*OA*OB*cos(r) , avec r l'angle entre (OA) et (OB) => r=-π/3 ;
OA=3,59 et OB=3,11 . L'application numérique me donne OC≈5,81 .

* Calcul de la phase initiale Φ de i.
soit C' le projeté orthogonal de C sur (Ox) et B' celui de B.

Dans le triangle OCC' , sinΦ=CC'/OC .
OACB étant un paralèllogramme, BB'=CC' or BB'=OB*sin(-π/3)
<=> sinΦ=OB*sin(-π/3)/OC

En application numérique, Φ≈-27,63°≈-0,48 radians.

Donc i(t)=5,81cos(100\pi*t-0,48) A.

Circuit RLC

Posté par
vanoisere : Circuit RLC 28-09-21 à 21:56

Non ! i1(t) est en avance de phase de /2 par rapport à u(t). Cela ressemblerait plutôt au diagramme ci-dessous.

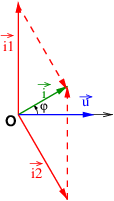
Circuit RLC

Posté par
fidele11re : Circuit RLC 29-09-21 à 08:22

Je pensais qu'on peut parler du déphasage entre deux grandeurs trigo si elles ont la même fonction trigo.

Ainsi dans ce cas de figure, l'angle entre le vecteur OA et le vecteur OB est π/2 - π/6=5π/6
On trouve donc avec la formule précedente OC=6,7.
Et le déphasage Φ entre i(t) et u(t) est tel que sinΦ=(OB.sin(-π/3))/OC
=> Φ=-0,49 radians.

Posté par
fidele11re : Circuit RLC 29-09-21 à 08:24

je voudrais dire

Citation :
l'angle entre le
vecteur OA et le vecteur OB est π/2 -
(-π/3)=5π/6

Posté par
vanoisere : Circuit RLC 29-09-21 à 11:52

Citation :
Je pensais qu'on peut parler du déphasage entre deux grandeurs trigo si elles ont la même fonction trigo.

C'est bien pour cela qu'à la dernière ligne de mon message du  27-09-21 à 22:53, j'ai transformer le cosinus en un sinus en ajoutant /2 !

Posté par
fidele11re : Circuit RLC 30-09-21 à 09:25

Okay d'accord .


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !