Inscription / Connexion Nouveau Sujet
Circuit RLC.
Bonsoir ,
Merci d'avance. 
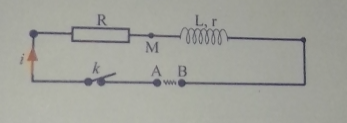
Pour déterminer les valeurs des grandeurs caractéristiques d'un circuit RLC , on étudie un circuit alimenté par une tension sinusoïdale de fréquence f = 50 Hz , de valeur efficace. Les mesures effectuées par un technicien ont donné : UAB = 173 , 2 V ; UAM= 100 V.
Données : ;
;
;
et
;
.
1) Construire le diagramme de Fresnel de ce circuit.
2) Déterminer la valeur de l'intensité efficace du courant qui traverse le circuit.
3) Évaluer graphiquement en degrés , les valeurs des phases ,
,
.
4) En déduire les valeurs de la résistance r et de l'inductance L de la bobine utilisée.
1) J'ai du mal à déterminer les vecteurs du conducteur ohmique et du circuit RLC. Le reste ça va.
Bonsoir
Commence par établir les expressions théoriques en fonction de i(t) des différentes tensions. Tu pourras ensuite tracer les vecteurs de Fresnel.
Tu connais la loi d'Ohm pour obtenir l'expression de uAM(t). Pour uMB(t) : tu peux considérer la bobine comme l'association en série de la résistance r et de l'inductance L.
Revois bien ton cours sur le sujet.
À titre de vérification, tu pourrais écrire ici les expressions des tensions instantanées. Tu as dû étudier en cours comment associer à une tension instantanée sinusoïdale un vecteur de Fresnel.
Ok. Reste à établir l'expression de L.di/dt et à tracer la somme des 3 vecteurs associés à R.i, à R.i et à L.di/dt. Apparemment, les vecteurs sont fournis. Tu peux scanner et poster ici le schéma.
Si : :
Tu peux maintenant tracer l'allure général des vecteurs de Fresnel mais l'énoncé parle à la question 3 de mesures graphiques. Les vecteurs de Fresnel doivent donc être fournis ; d'ailleurs une échelle est précisée...
Du coup il s'agit d'une erreur de la part de l'énoncé ?
Plus exactement d'un oubli. Sans le diagramme de Fresnel : impossible de résoudre l'exercice !
S'il s'agit juste d'un exercice d'entraînement, tu peux utiliser le diagramme ci-dessous. J'ai choisi arbitrairement :
= 46,1°
Il me semble préférable de poser :
puis de poser :
uAB=uAM + uMB
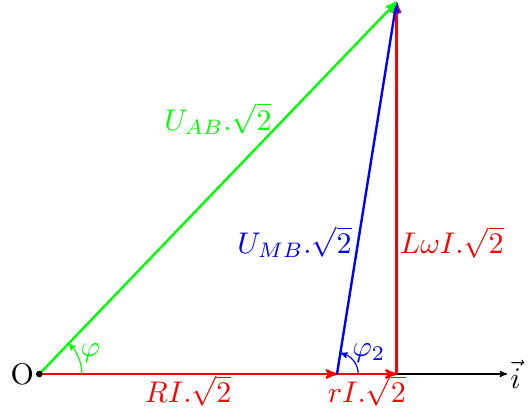
Pour construire le diagramme de Fresnel à l'échelle sans connaître aucun des angles, il te manque une donnée : par exemple : la valeur efficace de la tension uMB qui peut se noter : UMB.
Ah oui , j'ai sauté ; UAM=UMB= 100 V
J'espère que tu es conscient tu temps que ce simple oubli à fait perdre, aussi bien à toi qu'à moi-même...
Tout devient simple maintenant : les vecteurs de Fresnel associé à uAM (en rouge) et à uMB (en bleu) ont la même norme (6cm si on choisit d'associer à la norme du vecteur la valeur efficace plutôt que la valeur maximale). Le vecteur associé à uAB aura une norme 1,732
3 fois plus grande. Facile alors de tracer ces vecteurs en se servant d'une règle graduer et d'un compas. Tu peux ensuite mesurer les angles. Tu pourrais aussi facilement les calculer sachant que tu as tracé un triangle isocèle et que 
Annuler
connectez vous