Inscription / Connexion Nouveau Sujet
Circuit RLC
Bonjour, je bloque sur cet exercice:
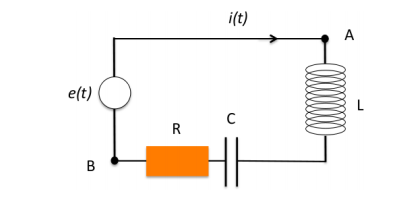
On considère le circuit donné ci-dessous alimenté par un générateur de tension sinusoïdale : e(t) de fréquence f=50Hz. Les éléments du circuit sont tels que R = 500Ω, L = 0,1 H et C = 1 µF.
La valeur efficace du courant traversant le circuit est Ieff = 0.03 A. En choisiant i(t) de la forme i(t) = IM cos ωt, on cherche à déterminer e(t).
1°) Déterminer la valeur de IM, et l'impédance totale ZAB correspondant à l'association de R, L et C. Mettre ZAB sous la forme module et argument.
2°) En déduire l'expression de e(t) et l'écrire sous la forme e(t) = EM cos (ωt + φ). Calculer EM et φ.
tout ce que je suis capable de trouver, c'est ZAB = R +jL +1/jC
+1/jC
Pouvez vous m'aider. merci
IM = Ieff * V2 = 0,03 * V2 = 0,0424 A
f = 50 Hz --> w = 2Pi.f = 100.Pi rad/s
Z = R + jwL + 1/(jwC)
Z = R + j(wL - 1/(wC))
Z = 500 + j(0,1*100.Pi - 10^6/(100.Pi))
Z = 500 - 3151.j
|Z| = V(500² + 3151²) = 3191 ohms
e = Z.i
arg(e) = arg(Z) + arg(i)
EM = |Z| * IM
EM = 3191 * 0,0424 = 135 V
arg(Z) = arctg(-3151/500) = - 1,216 rad
arg(i) = 0
arg(e) = - 1,216 rad (Phi)
e(t) = 135 * cos(100.Pi.t - 1,216)
-----
Sauf distraction. 


