Inscription / Connexion Nouveau Sujet
circuit RL, RLC
bonjour à tous, pouvez vous m'aider à résoudre cette exo , merci d'avance
on veut connaitre les caractéristiques électriques L (inductance) et r (résistance) d'une bobine d'alluamage B.
on branche cette bobine en série avec un interrupteur K aux bornes d'un générateur idéal de tension continue E=6V
question : établir l'équation différentielle ( écrire les lois d'ihm pour chaque dipôle)donnant l'intensité du courant i(t) dans le circuit lorsque ferme l'interrupteur.
que signifie une équation différentielle de l'intensité?
Uam= Uab+Ubm
E=Li'+Ri
i(t)= A(1-exp(-t/ ))
))
i'(t)= A(1/ )exp(-t/
)exp(-t/ )
)
résultat final:  = L/R constante de temps
= L/R constante de temps
je ne comprends pas i(t), i'(t) et le résultat final
merci de m'aider a++ 
salut, merci d'avoir prêté attention au message
oui je ne sais pas ce que signifie "équation différentielle "
tu es en licence de quoi ?
une équation différentielle c'est une équation qui lie une fonction à ses dérivées. Ici c'est l'équation différentielle de l'intensité, donc une équation qui lie i(t) à i'(t) qui est sa dérivée par rapport au temps
tu as compris ce que c'était une équa diff maintenant ?
tu as compris comment arriver E = L.i' + R.i ?
oui je comprends, jte remercie 
autre question : que signifie concrètement la dérivée par rapport au temps ? désolé de te posé une question "idote"
oui je comprends E = L.i' + R.i
mais pas la suite 
tu sais ce que c'est une dérivée ?
i' est la dérivée de i. Ici la variable par rapport à laquelle on dérive est "t", c'est à dire le temps (quand on dérive f(x) c'est une dérivée par rapport à x)
Quand tu as E = L.i' + R.i alors il faut lire ton cours, et savoir qu'il existe des formes de solution connue pour ce genre d'équation.
le cours dit :
"soit y une fonction de x, alors la solution de l'équation différentielle y' = a.x+b où a et b sont des constantes est :
y(x) = A.e^(a.x) - b/a où A est une constante à déterminer.
si tu réécris E=Li'+Ri, tu vois que :
i' = -R/L.i + E/L
là tu peux identifier avec la forme que je t'ai donné plus haut : a = -R/L et b = E/L
tu vas alors trouver tau = L/R
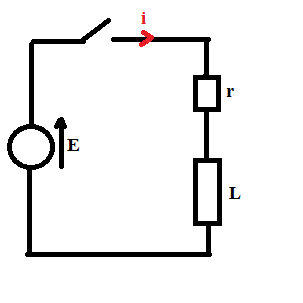
On ferme l'interrupteur à l'instant t = 0
Equation de la maille: E - ri - L.di/dt = 0
L.di/dt + Ri = E (dans ta réponse, on a noté i' pour di/dt, soit la dérivée de i par rapport au temps)
di/dt + (R/L)i = E/L
C'est l'équation différentielle donnant l'intensité du courant i(t) dans le circuit lorsque l'interrupteur est fermé.
La condition initiliale est :
i(0) = 0 (courant nul à l'instant initial à cause de la présence de l(inductance L).
-----
Il s'agit donc de résoudre l'équation di/dt + (R/L)i = E/L
a) solutions de l'équation homogène (avec second membre = 0):
di/dt + (R/L)i = 0
i = C.e^((-R/L)t) avec C unc constante réelle.
b) solution particulière de l'équation compèlte, soit donc de di/dt + (R/L)i = E/L
Une solution est : i = E/R
c) Solutions générales de di/dt + (R/L)i = E/L
Ces solutions sont la somme de celles trouvées aux point a et b ci-dessus.
i(t) = E/R + C.e^((-R/L)t)
Il faut maintenant trouver la valeur de C à l'aide de la condition initiale : i(0) = 0
E/R + C.e^((-R/L)*0) = 0
E/R + C = 0
C = - E/R
On a donc finalement :
i(t) = E/R - (E/R).e^((-R/L)t)
i(t) = (E/R).(1 - e^((-R/L).t))
-----
Cà, c'est la manière de faire ... si on a les bases suffisantes en math.
Si ce n'est pas le cas, parfois, il suffit de savoir trouver l'équation différentielle, soit di/dt + (R/L)i = E/L (qui est équivalente à E = L.i' + R.i)
Et puis, si le prof est gentil (ou sait que le niveau en math dans les études faites n'est pas suffisant ou pas encore acquis), il donne la forme de la solution, soit i(t) = A(1 - e^(-t/tau)) ... et il ne reste alors qu'à trouver les valeurs de A et Tau qui conviennent.
On fait alors ainsi :
i(t) = A(1 - e^(-t/tau))
on derive par rapport au temps et on obtient :
i' = (A/tau).e^(-t/tau)
on remplace, dans E = L.i' + R.i, i et i' par ce qu'on a trouvé
E = L.(A/tau).e^(-t/tau) + R.A(1 - e^(-t/tau))
E = A.R. + (AL/tau - AR).e^(-t/tau)
Pour que ce soit Vrai pour toute valeur de t > 0, on a alors :
E = AR
et (AL/tau - AR)
---> A = E/R et tau = L/R
-----
Sauf distraction. 
a) solutions de l'équation homogène (avec second membre = 0):
di/dt + (R/L)i = 0
i = C.e^((-R/L)t) avec C unc constante réelle.
pourquoi e^((-R/L)t) ?
b) solution particulière de l'équation compèlte, soit donc de di/dt + (R/L)i = E/L
Une solution est : i = E/R
POURQUOI "di/dt" a disparu ?
merci de me répondre
pourquoi e^((-R/L)t) ?
di/dt + (R/L)i = 0 est une équation à variables séparables :
di/dt = -(R/L)i
di/i = -(R/L)dt
en intgrant --->
ln|C1.i| = -(R/L)t
C1.i = e^(-(R/L)t)
i = (1/C1).e^(-(R/L)t)
et en posant C = 1/C1 -->
i = C.e^(-(R/L)t)
-----
POURQUOI "di/dt" a disparu ?
Ici, il s'agit de trouver UNE solution particulière à di/dt + (R/L)i = E/L
i = E/R est une telle solution particulière, en effet,
avec i = E/R, on a di/dt = 0 (puisque E/R est une constante (ne dépend pas de t) et que la dérivée d'une constante est nulle).
Et donc en remplaçant i par E/R et di/dt par 0 dans di/dt + (R/L)i = E/L, on trouve :
0 + (R/L)*(E/R) = E/L
E/L = E/L ... qui montre que i = E/L satisfait bien l'équation di/dt + (R/L)i = E/L ...
Et que donc i = E/R est bien UNE solution particulière de l'équation di/dt + (R/L)i = E/L
-----
Ces notions étaient normalement vues dans le Secondaire (1ère ? ou Terminale) ...
Tu devrais aller relire ces cours ... ou bien chercher les explications sur ce site dans les fiches de Math.





