Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

circuit RL avec lampe temoin

Posté par
alicia062 24-09-13 à 12:07

Bonjour

Voilà j'ai un exercice sur un circuit RL avec lampe témoin . Je n'arrive pas à le refaire ici(Mais pour le trouver il suffit de taper sur google "*** effacé ***" et cliquer sur le 2ieme lien "*** effacé ***" et mon exercice est le dernier )

Et je me demandais si pour exprimer i (cas où l'interrupteur est fermé) , nous pouvions le faire en fonction de iL ? Je pense que non mais dans ce cas je ne vois pas comment faire pour avoir une expression de i sans avoir iL ou i' (courant dans le générateur)

Je ne sais pas si j'ai été assez clair.

Pouvez vous m'aider à régler ce petit problème.

Je ne vois vraiment pas comment faire !!
Aidez moi S'IL VOUS PLAIT


MERCI!

Edit Coll

Posté par
gbm Webmasterre : circuit RL avec lampe temoin 24-09-13 à 12:15

Salut,

La règle du forum est de recopier intégralement l'énoncé + questions de l'exercice + schéma de la situation.

Merci

Posté par
alicia062re : circuit RL avec lampe temoin 24-09-13 à 14:33


D'accord je ne savais pas autant pour moi.
Alors voilà l'énoncé

Considérons le montage suivant. Calculer le courant i(t) dans la lampe :
1)en t =0+, juste après la fermeture de K

2) lorsque le régime permanent est atteint;
3)juste après l'ouverture de K
(l'ouverture a lieu une fois le régime permanent précédent atteint).

Sachant que la lampe ne s'allume que pour i>E/8R quel peut être son rôle? On supposera la lampe équivalente électriquement à une résistance.

Par contre pour le schéma du circuit je ne sais pas comment le reproduire et je n'arrive pas à le coller .
Je vais donc vous le décrire:
Il y a un circuit RL (une bobine avec une résistance R, un générateur avec une autre résistance R et un interrupteur K, cet ensemble forme une maille)
Et au borne de la bobine et de la résistance nous avons une lampe que l'on considère comme une résistance de 4R , et cet ensemble forme une autre maille
J'ai considéré i' comme l'intensité circulant dans le générateur iL dans la bobine et i dans la lampe

Voilà j'espère que vous pourrez vous visualiser le circuit .

Et ma question reste la même

Posté par
Aragornre : circuit RL avec lampe temoin 24-09-13 à 17:06

Bonjour,
Le circuit doit ressembler au schéma ci-dessous... si j'ai bien compris...
Il suffit d'appliquer les lois des mailles et des noeuds. On trouve une équation différentielle en i1.

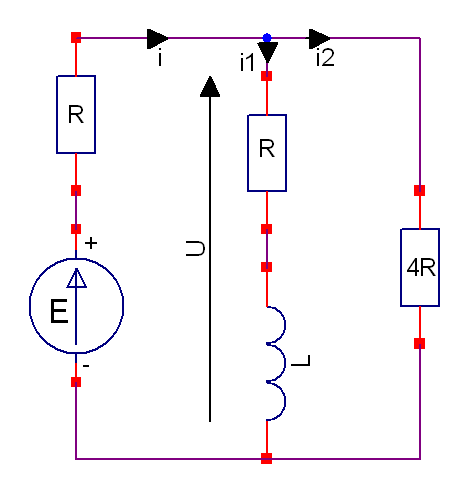
circuit RL avec lampe temoin

Posté par
alicia062re : circuit RL avec lampe temoin 24-09-13 à 21:21

Oui c'est bien ce schéma .
Mais justement nous ce que l'on veut c'est une expression en i2 pas avec i1

Posté par
gbm Webmasterre : circuit RL avec lampe temoin 24-09-13 à 21:27

En général, pour ce genre d'exercice, il faut appliquer la loi des mailles à toutes les mailles disponibles dans le circuit (ici j'en vois au moins trois) et la loi des noeuds

Posté par
Aragornre : circuit RL avec lampe temoin 24-09-13 à 21:40

Bonsoir gbm,
Tout à fait d'accord...
Alicia, on est obligé de calculer i1 puis calculer i2 ensuite...
La 1ère loi la plus facile à trouver est :
i\,=\,i_1\,+\,i_2

Posté par
Aragornre : circuit RL avec lampe temoin 24-09-13 à 21:42

Ensuite, soit tu écris les lois des mailles (de toutes les mailles), soit tu écris la tension U de 3 façons différentes...

Posté par
alicia062re : circuit RL avec lampe temoin 24-09-13 à 22:32

C'est bon je crois avoir reussi et j'obtiens l'expression suivante pour i2

i2(t)= (E/R)*(e(t/3) -1)

Mais cette expression me semble bizarre , elle n'est pas celle que l'on obtient habituellement ?
Est ce que vous pensez que cela est juste?

Posté par
alicia062re : circuit RL avec lampe temoin 24-09-13 à 22:37

Tout d'abord MERCI de m'accorder de votre temps pour me répondre

Ensuite j'ai également un autre problème  pour la question où K est ouvert .

J'ai bien trouvé l'expression de i  (i=A*e(-5t/)  Mais je sais pas quelle condition initiale dois-je prendre pour trouver A

Posté par
Aragornre : circuit RL avec lampe temoin 24-09-13 à 22:58

est égal à quoi ?

Posté par
Aragornre : circuit RL avec lampe temoin 24-09-13 à 23:07

\Large \tau\,=\,\frac{R}{L}, je suppose...

Mon calcul me donne le résultat suivant :
\Large i_2(t)\,=\,\frac{E}{9R}\,\left(1\,-\,e^{-\frac{9R}{5L}t}\right)

Citation :
Ensuite j'ai également un autre problème  pour la question où K est ouvert .

Dois-je comprendre que, dans un premier temps, on ferme l'interrupteur et, dans un deuxième temps, on l'ouvre ?

Posté par
alicia062re : circuit RL avec lampe temoin 24-09-13 à 23:16

Ah bon ?
Je t'explique comment j'ai fait :
J'ai dabord exprimer  i1 en fonction de i2  
J'obtiens i1=3i2-E/r
Apres en écrivant la loi des mailles j'obtient cette expression
di/dt=(1/3)i + E/3L  
Est ce que jusque ici on es daccord?

Oui =L/R

Oui dans le premier cas l'interrupteur était fermé
Puis on l'ouvre

Posté par
Aragornre : circuit RL avec lampe temoin 25-09-13 à 13:52

Je n'ai pas le temps de te répondre avant ce soir mais i1=3i2-E/r  me paraît faux a priori.

Posté par
alicia062re : circuit RL avec lampe temoin 25-09-13 à 15:07

C'est bon j'ai trouvé mon erreur , et je trouve bien l'expression que tu a cité précédemment.
Ensuite pour la suite c'est à dire quand l'interrupteur est ouvert j'obtiens:
i=(E/9R)*e(-5t/)

Par contre pour la dernière question (Sachant que la lampe ne s'allume que pour i>E/8R quel peut être son rôle? On supposera la lampe équivalente électriquement à une résistance.)
Je ne sais pas si il faut faire un calcul ou une justification suffit
C'est à dire:
Pour pouvoir être avertie (lampe s'allume) d'une surchage.

Posté par
alicia062re : circuit RL avec lampe temoin 25-09-13 à 15:08

Encore une fois merci du temps que tu m'accordes pour me répondre  Aragorn !

Posté par
Aragornre : circuit RL avec lampe temoin 25-09-13 à 22:49

Désolé... a priori, j'ai mélangé deux formules...
Pour i2, je trouve :
\Large i_2(t)\,=\,\frac{E}{9R}\,\left(1\,+\,\frac{4}{5}\,e^{-\frac{9R}{5L}t}\right)
J'ai fait le calcul de deux façons :
1) En calculant i1 et ensuite i2
2) En calculant i2 directement
Mais, en fait, je n'ai pas répondu exactement aux questions posées...

Citation :
Calculer le courant i(t) dans la lampe :
1)en t =0+, juste après la fermeture de K
2) lorsque le régime permanent est atteint;
3)juste après l'ouverture de K
(l'ouverture a lieu une fois le régime permanent précédent atteint).

1)
En   t\,=\,0^{\,+\,}  :
Le courant dans la bobine est nul donc   \large i_2(0^{\,+\,})\,=\,\frac{E}{R\,+\,4R}
\Large i_2(0^{\,+\,})\,=\,\frac{E}{5R}
2)
Lorsque le régime permanent est atteint, c'est comme si la bobine n'était pas là...
On a donc  \Large R\,//\,4R\,\Rightarrow\,R\,//\,4R\,=\,\frac{4R\times R}{4R+R}\,=\,\frac{4R^2}{5R}\,=\,\frac{4}{5}\,R

\Large i(+\infty)\,=\,\frac{E}{R+\frac{4}{5}\,R}\,=\,\frac{5E}{9R}
Donc, d'après le diviseur de courant :
\Large i_2(+\infty)\,=\,i(+\infty)\,\frac{R}{R+4R}\,=\,\frac{5E}{9R}\,\frac{1}{5}\,=\,\frac{E}{9R}
3)
Après ouverture de l'interrupteur quand le régime permanent a été atteint, le courant dans la bobine doit s'écouler dans la lampe :
\Large i_2(0^{\,+\,})\,=\,-\,\frac{E}{9R}

La lampe est allumée au début et s'éteint lorsque le régime permanent est atteint ou un peu avant \large \left(\frac{E}{9R}\,<\,\frac{E}{8R}\,<\,\frac{E}{5R}\right).
Avec la valeur de i_2(t), on peut calculer quand elle s'éteint.

On retrouve les résultats avec la solution de l'équation différentielle donnée au début.
Il n'est donc pas absolument indispensable d'établir et de résoudre l'équation différentielle pour répondre aux questions.
Je calculerai cependant i2(t) après l'ouverture de l'interrupteur.

Posté par
alicia062re : circuit RL avec lampe temoin 26-09-13 à 14:43

Je ne comprend vraiment pas ta nouvelle expression de i2 puisque je l'ai refait plusieurs fois et je ne trouve pas ce que tu dit.  Et pour moi ta première expression est juste!

Je ne vois pas d'où sort ton 4/5 ?
J'ai trouvé que  i=(E/R) -4i Donc avec la loi des nœuds i1=(E/R)-5i2
Puis en appliquant la loi ds mailles en remplaçant avec la définition de la bobine j'obtiens l'équation différentiel suivante
di/dt+(9/5)=E/5L
Et qd on résout cette équation , on retrouve l'expression que tu as trouvé au début.

Et pour la dernier question , je pensais plus à une application concrète de l'utilité de cette lampe Non ?

Posté par
Aragornre : circuit RL avec lampe temoin 26-09-13 à 22:08

Voici les 4 équations :
\Large i\,=\,i_1\,+\,i_2\qquad (1)\,\Rightarrow\,i_1\,=\,i\,-\,i_2

\Large E\,-\,R\,i\,-\,R\,i_1\,-\,L\,\frac{di_1}{dt}\,=\,0\qquad (2)

\Large -4\,R\,i_2\,+\,L\,\frac{di_1}{dt}\,+\,R\,i_1\,=\,0\qquad (3)

\Large E\,-\,R\,i\,-\,4\,R\,i_2\,=\,0\qquad (4)\,\Rightarrow\,i\,=\,\frac{E}{R}\,-\,4\,i_2

\Large (2)\,\Rightarrow\,E\,-\,R\,i\,=\,R\,i_1\,+\,L\,\frac{di_1}{dt}
\Large (1)\,\Rightarrow\,E\,-\,R\,(i_1+i_2)\,=\,R\,i_1\,+\,L\,\frac{di_1}{dt}
\Large E\,-\,R\,i_2\,=\,2\,R\,i_1\,+\,L\,\frac{di_1}{dt}
\Large i_1\,=\,i\,-\,i_2\,\Rightarrow\,E\,-\,R\,i_2\,=\,2\,R\,i\,-\,2\,R\,i_2\,+\,L\,\frac{di}{dt}\,-\,L\,\frac{di_2}{dt}
\Large E\,=\,2\,R\,\left(\frac{E}{R}\,-\,4\,i_2\right)\,-\,R\,i_2\,+\,L\,\frac{d}{dt}\left(\frac{E}{R}\,-\,4\,i_2\right)\,-\,L\,\frac{di_2}{dt}
\Large E\,=\,2\,E\,-\,8\,R\i_2\,-\,R\,i_2\,-\,4\,L\,\frac{di_2}{dt}\,-\,L\,\frac{di_2}{dt}
\Large E\,-\,9\,R\,i_2\,-\,5\,L\,\frac{di_2}{dt}\,=\,0
\Large 5\,L\,\frac{di_2}{dt}\,+\,9\,R\,i_2\,\,-\,E=\,0
Tu résous l'équation différentielle de la façon que tu veux. Je propose de la résoudre à la "sauce Terminale" :
\Large \frac{di_2}{dt}\,=\,-\,\frac{9}{5}\,\frac{R}{L}\,i_2\,+\,\frac{E}{5\,L}
\Large i_2(t)\,=\,K\,e^{-\,\frac{9}{5}\frac{R}{L}t}\,+\,\frac{E}{9\,R}

\Large i_2(0)\,=\,\frac{E}{5R}\,=\,K\,+\,\frac{E}{9R}\,\Rightarrow\,K\,=\,\frac{4}{5}\,\frac{E}{9R}

\Large i_2(t)\,=\,\frac{4}{5}\,\frac{E}{9R}\,e^{-\,\frac{9}{5}\frac{R}{L}t}\,+\,\frac{E}{9R}

\Large \boxed{i_2(t)\,=\,\frac{E}{9R}\,\left(1\,+\,\frac{4}{5}\,e^{-\,\frac{9}{5}\frac{R}{L}t}\right)}

Sauf erreur de recopie éventuelle...

Dans le premier calcul que j'ai fait, j'avais calculé i1(t) d'abord et j'en avais déduit i2(t). J'ai obtenu le même résultat, bien sûr...

Posté par
alicia062re : circuit RL avec lampe temoin 27-09-13 à 13:36

Je comprend mieux
Merciii  beaucoup !!

Posté par
Aragornre : circuit RL avec lampe temoin 27-09-13 à 20:16

J'ai oublié de préciser pourquoi   \Large i_2(0)\,=\,\frac{E}{5R}
A t = 0, le courant est nul dans la bobine (i1 = 0) (c'est une propriété des bobines).
Donc il reste un générateur E , une résistance R et une résistance 4R en série (donc 5 R).
D'où le courant   \Large i_2(0)\,=\,\frac{E}{5R}

Posté par
Aragornre : circuit RL avec lampe temoin 28-09-13 à 23:46

Pour l'ouverture de l'interrupteur...
Je savais bien qu'il fallait calculer i1 avant avec l'interrupteur fermé. On va en avoir besoin. On verra pourquoi tout à l'heure.

\Large E\,-\,R\,i\,-\,4\,R\,i_2\,=\,0\qquad (4)\,\Rightarrow\,i\,=\,\frac{E}{R}\,-\,4\,i_2\,\,

\Large i_2(t)\,=\,\frac{E}{9R}\,\left(1\,+\,\frac{4}{5}\,e^{-\,\frac{9}{5}\frac{R}{L}t}\right)
\Large i_1\,=\,i\,-\,i_2\,=\,\frac{E}{R}\,-\,4\,i_2\,-\,i_2\,=\,\frac{E}{R}\,-\,5\,i_2

\Large i_1\,=\,\frac{E}{R}\,-\,5\,\frac{E}{9R}\,\left(1\,+\,\frac{4}{5}\,e^{-\,\frac{9}{5}\frac{R}{L}t}\right)
\Large i_1(t)\,=\,\frac{4}{9}\,\frac{E}{R}\,\left(1\,+\,\frac{4}{5}\,e^{-\,\frac{9}{5}\frac{R}{L}t}\right)
Donc :
\Large i_1(+\infty)\,=\,\frac{4}{9}\,\frac{E}{R}

On n'a plus qu'une seule maille :
\Large R\,i_1\,+\,L\,\frac{di_1}{dt}\,-\,4\,R\,i_2\,=\,0
Et :
\Large i_1\,+\,i_2\,=\,0\,\Rightarrow\,i_1\,=\,-\,i_2
Donc :
\Large -\,R\,i_2\,-\,L\,\frac{di_2}{dt}\,-\,4\,R\,i_2\,=\,0
\Large L\,\frac{di_2}{dt}\,=\,-\,5\,R\,i_2
\Large \frac{di_2}{dt}\,=\,-\,\frac{5\,R}{L}\,i_2
d'où :
\Large i_2(t)\,=\,K\,e^{-\,\frac{5\,R}{L}t}
i2(0) est la valeur de i1(+) de l'épisode précédent (interrupteur fermé) au signe près :

\Large i_2(0)\,=\,-\,\frac{4}{9}\,\frac{E}{R}\,=\,K

\Large \boxed{i_2(t)\,=\,-\,\frac{4}{9}\,\frac{E}{R}\,e^{-\,\frac{5\,R}{L}t}}


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !