Niveau maths sup

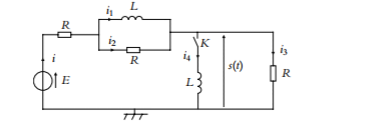
Circuit RL

Posté par
Miraa98 27-12-17 à 18:56

On nous demande de trouver la valeur de i4,i1,i,i2,i3 à t=0+.
Dans la correction il a consideré i4(0+)=0 d'apres la continuité de l'intensité aux bornes de la bobine .mais il a pris i1(0+)=E/2R.Merci de m'expliquer comment il a obtenu ce resultat

Circuit RL

Posté par re : Circuit RL 27-12-17 à 19:05

Bonjour

Citation :
Dans la correction il a consideré i4(0+)=0 d'apres la continuité de l'intensité aux bornes de la bobine .mais il a pris i1(0+)=E/2R

La situation t<0 correspond à K ouvert. Dans ce cas, i4=0 mais i1=E/2R...
Je te laisse réfléchir à cela et poster éventuellement à nouveau si tu ne vois pas comment obtenir ce résultat.
Indication : en régime permanent, la tension aux bornes de la première bobine est u_L=L(di₁/dt)=0 ; la première bobine se comporte alors comme un simple fil conducteur de résistance négligeable...

Posté par re : Circuit RL 27-12-17 à 19:13

Lire, bien entendu : i1(0+) = E/(2R)

Posté par re : Circuit RL 27-12-17 à 19:29

Mercii j'ai compris☺

Posté par re : Circuit RL 27-12-17 à 21:18

Pour i(0+) j'ai trouvé qu'elle egale a E/6R .par contre il est écrit dans la correction qu'elle est égale à E/2R.pouvez vous me dire pourquoi E/2R?

Posté par re : Circuit RL 27-12-17 à 22:01

Raisonnons d'abord sur le régime permanent correspondant à t<0 avec K ouvert. Comme déjà expliqué : la bobine de droite n'intervient pas ( $i_{4}=0$ ) et la première bobine (celle de gauche) se comporte comme un fil de résistance négligeable. Cette bobine court-circuite la résistance R en dérivation avec elle ( $i_{2}=0$ ). Le circuit est donc équivalent à un générateur idéal de tension de f.é.m. E alimentant deux résistances R en série. De façon évidente pour t<0 :

$i=i_{1}=i_{3}=\frac{E}{2R}$

À la fermeture de (K), chaque bobine assure la continuité de l'intensité dans sa branche :

$i_{4(0+)}=0\quad;\quad i_{1(0+)}=\frac{E}{2R}$

Les résistances n'imposent aucune condition particulière ; elles vérifient la loi d'Ohm à chaque instant. La loi des nœuds conduit à :

$i_{(0+)}=i_{1(0+)}+i_{2(0+)}=i_{3(0+)}+i_{4(0+)}$

Soit :

$i_{(0+)}=\frac{E}{2R}+i_{2(0+)}=i_{3(0+)}$

La loi des mailles conduit à :

$E=R.i_{(0+)}+R.i_{2(0+)}+R.i_{3(0+)}=2R\left(\frac{E}{2R}+i_{2(0+)}\right)+R.i_{2(0+)}=E+3R.i_{2(0+)}$

Cela conduit à :

$i_{2(0+)}=0\quad;\quad i_{(0+)}=i_{3(0+)}=\frac{E}{2R}$

Posté par re : Circuit RL 27-12-17 à 22:09

J'ai fait une faute de calcul! Merci beaucoup pour votre effort

Posté par re : Circuit RL 28-12-17 à 09:40

Miraa98,

Il est important (et même capital) de connaître les priorités des opérations mathématiques et l'usage correct des parenthèses.

Lorsque tu écris : E/2R cela signifie $\frac{E}{2}R$

Si tu veux que ce soit $\frac{E}{2R}$ , alors une écriture correcte est : E/(2R)

Et surtout ne pense pas que c'est sans importance.

Voila un extrait de ce site (wiki) sur le sujet (pris ici : )

Circuit RL

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Circuit RL

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique