Bonjour Drash, et bonjour Coll,

moi je veux bien t'aider, mais sans l'enonce il faut reconnaitre que ce n 'est pas pratique... Il n'y a pas de generateur dans ton circuit, donc je suppose que l'un des condensateurs (sans doute Cb) est charge et qu'il se decharge dans l'autre lorsqu'on ferme l'interrupteur. Et on etudie l'evolution de la tension u(t) aux bornes de Ca : est-ce ca ? Je commence a plancher sur cette base-la, mais ce serait bien si tu pouvais taper l'enonce completement...

Prbebo.

Bonsoir,

Voici l'énoncé en question :

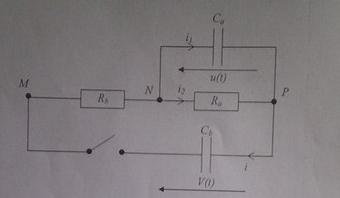
On considère le montage de la figure ci-dessous. On ferme l'interrupteur à t=0. Avant la fermeture, le condensateur Ca est déchargé alors que la tension aux bornes de Cb est Vo.

1) Etablir les relations Cb*[d(V)/dt] = ( u-V)/Rb et i = Ca*[d(u)/dt]+ [u/Ra]

2) Montrer que la tension u vérifie l'équation différentielle : d²u/dt² + (wo/Qo)d(u)/dt + wo²*u =0

où Qo et wo sont des constantes à déterminer en fonction de Ca, Cb, Ra et Rb.

3)

a) Montrer que les deux solutions du polynôme caractéristique sont des réels négatifs que l'on notera r1 et r2.

b) En déduire l'expression générale de u(t)

c) Montrer que i2 ( 0+ ) = 0 et i1(0+) = Vo/Rb

d) En déduire l'expression finale de u(t)

Bonjour,

Personne pour m'aider ?

Bonjour Drash,

si si, il y a moi, mais je n'ai pas eu le temps hier de te taper ma solution. Je coince encore sur la question 3a (je me demande s'il ne manquerait pas des valeurs numeriques des resistances et des condensateurs, car algebriquement je n'ai pas encore trouve).

Je te tape donc mes reponses des maintenant. On se revoit dans une petite heure.  Prbebo.

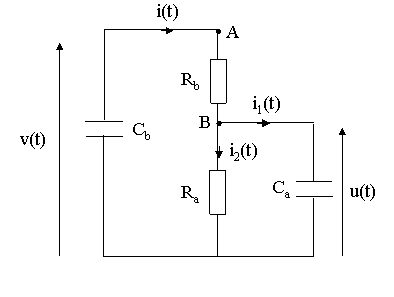
me revoila : tu peux suivre mes explications sur le schema ci-dessous, que j'ai repris du tien mais en y changeant V(t) en v(t), car en electronique on reserve la majuscule a des grandeurs constantes et la minuscule a des fonctions du temps. Ainsi i, v, u veulent dire i(t), v(t, u(t) : on n'est plus oblige d'ecrire (t) a chaque fois, ce qui fait gagner beaucoup de temps.
Je vais aussi te donner les expressions sans justification lorsqu'elles sont immediates.

Question 1 :
i = -Cb.dv/dt (1), le signe - venant du fait que Cb se decharge (donc v diminue avec t) ;
vA - vB = v - u = Rbi, soit i = (V - u)/Rb  (2).
De (1) et (2) on deduit Cb.dv/dt = (u - v)/Rb = -i  (3).
i = i1 + i2  (4) ;
i1 = Ca.du/dt (+, car Cb se charge donc u augmente avec t)  (5) ;
i2 = u/Ra  (6).
Des relations (4) a (6) on deduit i = Ca.du/dt + u/Ra  (7).

Question 2 :
de (3) et (7) je tire dv/dt = -i/Cb = (-1/Cb).(Ca.du/dt + u/Ra). J'ai donc une expression de dv/dt en fonction de la grandeur u cherchee.
En derivant (3) j'obtiens di/dt = (1/Rb).(dv/dt - du/dt) ;
En derivant (7) j'obtiens di/dt = Ca.d²u/dt² + 1/Ra.du/dt.
En egalant ces deux expressions de di/dt, et en remplacant dv/dt par son expression en focntion de u, j'obtiens une equation differentielle qui ne contient plus que u(t).
Je n'ai pas trop le temps de taper les calculs intermediaires... Voici a quoi j'arrive, apres avoir regroupe les termes et divise par Ca :
d²u/dt² + [1/RaCa + 1/RbCb + 1/RbCa].du/dt + u/(RaRbCaCb) = 0.
Sauf erreur bien sur, mais en tout cas cette relation est homogene.
Posons RaCaRbCb = 1/₀². Le crochet devant du/dt peut s'ecrire (RbCb + RaCa + RaCb)/(RaCaRbCb) = ₀².(RbCb + RaCa + RaCb). En le posant egal a ₀/Q₀, on en tire une expression de Q₀ : 1/Q₀ = ₀(RaCa + RbCb + RaCb). Je n'ai rien trouve de plus simple. On peut verifier que puisque ₀ se mesure en s^-1 et que les trois produits RC sont homogenes a des temps, le terme Q₀ n'a pas d'unite. Il aurait ete plus fute de modifier la definition de Q₀ pour avoir un terme pair devant du/dt, ce qui permettrait d'utiliser le discriminant reduit, mais bon... a signaler eventuellement a ton prof.

Question 3 :

a)  L'equation differentielle d²u/dt² + (₀/Q₀).du/dt + ₀²u = 0 admet pour discriminant = (₀/Q₀)² - 4₀² = ₀²(1/Q₀² - 4). Il s'agit de montrer que est positif, mais sans valeur numerique impossible de savoir ce que vaut la parenthese. A moins bien sur que j'aie fait une erreur de calcul quelque part...
Si on admet ce resultat, on ecrit r1 = (-₀/Q₀ - )/2 et r2 = (-₀/Q₀ + )/2. La racine r1 est visiblement negative. Quant a r2, puisque est plus petite que ₀/Q₀, elle est negative elle aussi. Et c'est une bonne chose, car les exponentielles figurant dans l'expression de u(t) ne doivent pas avoir d'exposant positif !

b)  l'expression generale de u est u(t) = A.exp(r1.t) + B.exp(r2.t). L'equation differentielle n'ayant pas de second membre sa solution est celle de l'equation homogene. Ceci revient a dire que u(t) -> 0 au bout d'un temps suffisamment long.

c)  Avec (6) on a obtenu i₂ = u/Ra. Or la tension aux bornes d'un condensateur doit rester continue, donc u(0^-) = u(0⁺). Ici, u(0^-) = 0 (Ca non charge), donc u(0) = 0 soit i₂(0) = 0.
Puisque i2(0) et nul, tout le courant i passe dans la capacite a l'instant 0. Or a t = 0⁺ vB - vM = u(0⁺) = 0 : le circuit, uniquement a cet instant, est equivalent a une source de tension V₀ en serie avec la resistance Rb. Donc i(0⁺) = V₀/Rb = i₁(0+).
La relation (5) donne (du/dt)(0⁺) = V₀/(CaRb).

Tu disposes ainsi de deux conditions initiales, l'une sur u(t) u(0) = 0, l'autre sur sa derivee du/dt. Tu peux donc sans pb ecrire deux relations qui donneront les expressions des constantes A et B.

Je te laisse finir (a vrai dire, il ne reste plus grand chose a faire !). Si tu trojuves uneerreur de calcul signale-la moi stp. Et lorsque tu auras la solution, mets-la sur le forum.

Si tu as d'autres questions a poser n'hesite pas.

Prbebo.

Bonjour prbebo,

2 ) En déroulant le calcul, je trouve  comme toi : d²u/dt² + [1/RaCa + 1/RbCb + 1/RbCa].du/dt + u/(RaRbCaCb) = 0.

Donc pas d'erreur de calcul manifestement.

c) Donc si je te suis bien quand tu écris : "donc u(0) = 0 soit i2(0) = 0." C'est bien i2(0+) = 0 ?

Sinon, je suis OK pour le raisonnement.

d) Voila ce que j'ai fait en suivant tes indications :

u(t) = A'.exp(r1.t) + B'.exp(r2.t)

Première  C.I : u(0-) = u(0+ )0 => 0 = A' = - B'

Deuxième CI :

du(0+)/dt = A'*r1*exp(0) + B'*r2*exp(0)

<=> A'*r1 + B'*r2 = du(0+)/dt

Or B'= -A' donc on a : A'(r1-r2) = du(0+)/dt
Soit A'(r1-r2) = Vo/(Ca*Rb)
Donc A'= Vo(r1-r2)/ ( Ca*Rb) = - B'

On a donc :



Trouves-tu le même résultat ?

Pour ta premiere question : oui en effet, c'est i2(0⁺). Cpdt, dans cet exercice i2(0⁺) = i2(0^-) = i2(0), car i2 = u/Ra et que u(t) est continu en t = 0. Moi j'ai l'habitude, donc je ne me suis pas embete avec les ⁺ et les ^-. Cependant dans ton corrige il vaudrait mieux en tenir compte.

pour d) : B' = -A' OK (tu aurais pu garder A et B car l'asterique ne sert a rien ici). En revanche, il me semble que A' = V₀/(CaRb)/(r1 - r2), et non x (r1-r2)... Sinon  c'et bien ca.

Je suis surpris qu'il n'y ait pas d'autres indications dans ton enonce, car il est manifeste que tel quel on ne peut pas conclure sur le signe de . Quand tu auras le corrige mets-le sur le forum car ca m'interesse vraiment.

Bon ben, je crois qu'on a fini...

A bientot peut-etre pour d'autres exercices sur les regimes transitoires (ou autres).

BB.

3)
d) Tu voulais plutôt écrire A'= Vo/ [( Ca*Rb)* ( r1-r2) ] ?


Sinon pour la première question, si je réponds par :

Pour ta remarque "A'= Vo/ [( Ca*Rb)* ( r1-r2) ] ?" : il me semble que ce que j'ai ecrit et ce que ce que tu me proposes sont identiques, car en maths l'ecriture a/(bc) est equivalente a a/b/c.

Pour le reste :
les relations que j'ai ecrites (1 a 7) traduisent ce qui se passe des que l'interrupteur est ferme : Cb se decharge donc v(t) diminue et sa derivee dv/dt est negative. Or cette derivee sert a exprimer le courant i(t) qui resulte de la variation de charge de Cb. Si on veut ecrire vA - vB = Rb.i, ecriture impliquant de compter i >0, on est contraint d'ecrire i = -Cb.dv/dt pour compenser le signe - de la derivee. C'est la seule facon de ne pas avoir de conflit entre les signes. Si tu en doutes, la meilleure maniere de te convaincre est de t'inciter a ecrire i = + Cb.dv/dt et de poursuivre la mise en equation du circuit : tu obtiendras des exponentielles a exposants positifs, ce qui est physiquement impossible.
Pour ta remarque 1i : tu as change le signe de i et permute u et V dans ma relation 2 : jusque la  ca semble etre coherent ; mais en ecrivant i = + i1 + i2, cette fois ca ne l'est plus puisque tu as change le signe de i mais pas celui de i2.

De meme : juste apres l'instant initial, puisque u qui etait nul devient positif ca signifie que le condensateur Ca se charge. Il est donc legitime d'ecrire i1 = + Ca.du/dt puisque si on ecrit i = i1 + i2, avec le courant i arrivant sur le noeud positif et le courant i2 >0 aussi, la coherence des notations impose i1 > 0).
La situation telle que je l'ai decrite traduit un etat reel du circuit, rencontre juste apres la fermeture de l'interrupteur. Il est possible qu'ulterieurement les sens des courants s'inversent (ce n'est pas le cas ici puisqu'il n'y a pas de regime oscillant, mais on peut trouver ca dans d'autres exercices). Peu importe puisque les courants et les tensions sont des variables algebriques. Les ecrire en connaissant leur signe a un instant donne permet de trouver l'equa diff qui fixera leur signe a un instant ulterieur. Je sais, ce n'est pas simple...

Prbebo.