Inscription / Connexion Nouveau Sujet
circuit RC
Bonsoir, je voudrais de l'aide dans ce problème
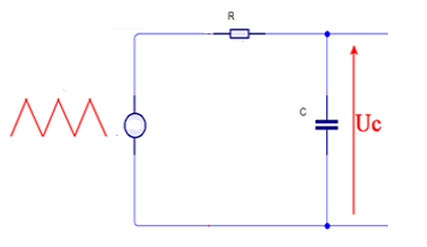
On a un circuit électrique RC , composé d'une résistance et d'un condensateur montés en série, alimenté par un signal électrique triangulaire
1-quel est la nature de tension Uc entre les borne de condensateur
2-comment se varier le courant qui circule dans le circuit
Bonsoir
Rigoureusement, il faut commencer par établir l'équation différentielle vérifiée par U c(t) en fonction de la tension e(t) fournie par le générateur. Il faut ensuite chercher les solutions de cette équation différentielle dans les deux cas :
Tension d'entrée fonction affine croissante de t :
Tension d'entrée fonction affine décroissante de t.
Cela dit, il y a des simplifications possibles si le produit R.C est très petit devant la demie période de la tension d'entrée.
Je te laisse réfléchir et proposer une solution...
Merci Vanoise,
j'essaie cette démonstration
on a :
ce qui nous donne
avec
on obtient:
la solution et de la forme
quant t tend vers l'infini on trouve
à t=0 on a on remplace dans l'équation différentielle; on trouve A=-B=-U
donc on a
on peut écrit U=at+b
après je ne sais pas
Il faut remplacer U par son expression en fonction de t avant de résoudre l'équation différentielle :
pendant une demie période puis :
pendant l'autre demie période. C'est assez délicat à résoudre. Il serait plus simple de commencer par résoudre l'équation différentielle vérifiée par i(t) mais cela ne semble pas correspondre à l'énoncé.
Je me pose quelques questions :
* le générateur en entrée est-il bien un générateur idéal de tension triangulaire ? Pas un générateur idéal de courant ?
* cet exercice est-il posé par ton professeur ou bien l'as-tu trouvé dans un livre pas nécessairement adapté à ton niveau ?
* En effet : cet exercice serait beaucoup plus facile à traiter et beaucoup plus intéressant à traiter après l'étude des filtres de type "RC"....
J'ai repris tes équations différentielles sans les vérifier : tu as oublié de diviser U par RC. Il serait plus simple d'écrire :
pendant une demie période puis :
pendant l'autre demie période.
Merci Vanoise;
pour le générateur je ne sais s'il est un générateur idéal de courant.
pour l'exercice je le trouve dans une ancienne série qui traite le comportement d'une capacité dans un circuit électrique
pour les équation différentielle
la solution générale
la solution particulière
à t=0 on a
donc
pendant l'autre demie période :
En supposant que le générateur soit un générateur de tension triangulaire, tes calculs sont corrects.Pour terminer, il faudrait déterminer les constantes en considérant que uc(t) est une fonction continue du temps (pas de discontinuité à chaque changement de demie période) et en considérant que uc(t) varie de façon alternative (valeur moyenne nulle sur chaque période). Il n'est pas alors indispensable d'écrire l'équation différentielle vérifiée par i(t) pour la résoudre. Plus simplement : i(t)=C.(duc/dt). Tout cela est très calculatoire... Très souvent, on demande de traiter les deux cas particuliers suivants :
1° : RC petit devant la demie période (fréquence faible) : le terme en RC.(duc/dt) reste petit devant uc(t) ; l'équation différentielle se dimplifie pour donner :
uc(t) U : uc est pratiquement égale à la tension d'entrée.
U : uc est pratiquement égale à la tension d'entrée.
2° : RC grand devant la demie période (fréquence élevée). C'est au contraire uc qui est négligeable devant RC.(duc/dt). L'équation différentielle simplifiée devient :
RC.(duc/dt) U=a.t +B ou -a.t+b'
U=a.t +B ou -a.t+b'
On obtient des arcs de parabole comme tension de sortie.
Pour visualiser tout cela , tu peux consulter ce site : ![]()
Choisis une tension d'entrée en triangle. Tu peux laisser pour R et C les valeurs par défaut de sorte que RC=10-4s.
Observe les signaux pour une fréquence voisine de 500Hz puis pour une fréquence voisine de 20000Hz (modifie éventuellement le gain de sortie pour une meilleure observation de la courbe uc(t).)


