Inscription / Connexion Nouveau Sujet
Circuit R,L,C parallèle.
Bonsoir,je poste ce message parce que j'aurai voulu le corrigé de cet exo long si possible,j'ai tenté de répondre quand j'ai pu.
Voici l'énoncé:
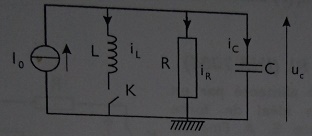
La figure ci-dessous donne le schéma du montage étudié,le générateur de courant est idéal,de courant de court-circuit I0 constant.
Les dipôles passif R,L,C sont idéaux.
A l'instant t=0,l'interrupteur est fermé instantanément et on cherche à déterminer l'évolution ultérieur des grandeurs électriques du réseau.
1)Déterminer par un raisonnement simple (pratiquement sans calcul) la tension Uc et ic,ir, et Uc dans les trois branches:
-a)Juste après la fermeture de l'interupteur(à t=0+).
-b)Au bout d'une durée très grande(t->).
2)établir l'équa.diff liant Uc à ses dérivées temporelles,on posera pour la suite ,2*
=
3)R=10k ;C=1
;C=1 F;.L=10mH.
F;.L=10mH.
.
Calculer la pulsation propre w0 et T0 ainsi que  .
.
Vérifié que le régime est pseudo périodique.
Que caractérise  ?
?
Préciser l'expression et la valeur du facteur de qualité Q.
4)Quelle est alors la forme de la solution?
Définir et calculer la pseudo pulsation w.
Compte tenu de la précision et des données,que peut-on dire des valeurs numérique comparé de w0 et w?
5)Déterminer en fonction des constantes w, ,I0 et R,l'expression complète de Uc(t).
,I0 et R,l'expression complète de Uc(t).
Et voici quelques-une de mes réponses:
1a)On sait que ic=Cduc/dt donc Uc= (ic/C).dt
(ic/C).dt
Mais vu que Uc=Ur=UL du fait que les tension de C,R,L sont égales(en parallèle)Uc=Rir=LdiL/dt.
On aurait peut voir aussi un diviseur de courant mais il n'y a pas que des résistances.
b)Je sais qu'on est en régime permanent mais j'ai pas trop compris ce régime peut-être faut-il transformé le circuit?.
3)w0=1/racine(RC)=31622rad/s.
T0=1/f0 et f0=w0/2 =49672s-1.;T0=2.01*10^-5.
=49672s-1.;T0=2.01*10^-5.
Ensuite, =1/(2RC).
=1/(2RC).
Après le régime est pseudo périodique si  <0
<0  étant le discriminant de l'équation
étant le discriminant de l'équation  [sup][/sup]+w0/Q+w0²=0.
[sup][/sup]+w0/Q+w0²=0.
Puis ensuite  c'est le facteur d'amortissement,et Q=1/2
c'est le facteur d'amortissement,et Q=1/2 ou 1/2m.
ou 1/2m.
4)La forme de la solution dans le cas pseudo périodique est alors Uc(t)=K.cos(wt+ )exp(-t/
)exp(-t/ ).
).
w=w0.racine(1-(1/4Q²)).
Bonsoir,
A t=0+, la situation est la même qu'à 0- à peu de choses près...
A t  +
+ :
:
As-tu des problèmes avec ces réponses ?
Bonjour,euh non ça va,je vois globalement pourquoi on a ça,mais qu'en est-il de mes autres réponses?
On a :
(1)
Et :
Et :
Et :
En dérivant l'équation (1) :
Je te laisse faire l'application numérique de la question 3.
OK pour le régime pseudo-périodique, le facteur de qualité Q et  .
.
Jusque là, ça te va ?

 !
!
