Inscription / Connexion Nouveau Sujet
circuit et condensateurS
Bonsoir,
J'ai des difficultés avec un devoir maison.
Voici l'énoncé :
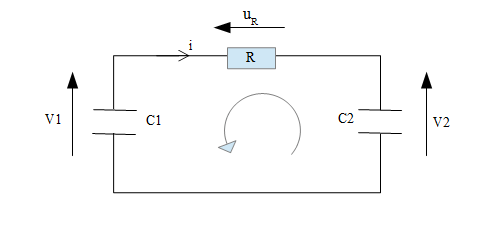
On considère le circuit électrique ci-dessous comprenant deux condensateurs de capacités respectives C1 et C2, montés en série avec une résistance R. A l'instant t=0, la tension V, aux bornes de C1 vaut V10 et la tension V2 aux bornes de C2 vaut V20.
J'ai mis les questions en gras et mes réponses en italiques
1. Donner trois expressions du courant i(t), l'une (1) en fonction de V1, V2 et R, l'autre (2) en fonction de C1 et dV1/dt et la troisième (3) en fonction de C2 et dV2/dt.
(1) i= - (V2-V1)/R
(2) i= - dq1/dt
(3) i= dq2/dt
2. En déduire que C1V1+C2V2 est une constante et l'exprimer en fonction des données. Quelle est la signification physique de cette constante ?
- C1*dV1/dt=C2*dV2/dt
0=C2*dV2/dt + C1*dV1/dt
J'ai fait l'intégrale des expressions qui étaient de chaque côté de la parenthèse et j'ai obtenu
cste= C1V1+C2V2 = q1+q2
Après je ne vois pas comment exprimer la constante en fonction des données de l'énoncé et sa signification physique........
3. Montrer que V1(t) est solution d'une équation différentielle de la forme :
dV1/dt +V1=A1
et déterminer les constantes et A1 en fonction des données.
En déduire l'expression de V1(t) puis celle de V2(t) et enfin de i(t). Préciser la signification physique des constantes A1 et et retrouver leurs expressions par un raisonnement physique.
J'ai fait une loi des mailles : V2+uR-V1=0
V2+R(C1*dV1/dt)-V1=0 mais ensuite je ne vois pas comment obtenir le résultat attendu.
Merci de votre aide !
Excusez-moi j'ai envoyé le message sans faire exprès et je n'avais pas fini de l'écrire donc voici le circuit en question.
1)
(1) i= (V1-V2)/R
(2) i= -C1.dV1/dt
(3) i= C2.dV2/dt
-----
2)
-C1.dV1/dt = C2.dV2/dt
On intègre :
-C1.V1 + K = C2.V2 (K étant une costante réelle)
C1.V1 + C2.V2 = K ... quel que soit t et donc notamment en t = 0
--> K = C1.V10 + C2.V20
K représente la charge présente dans l'ensemble des 2 condensateurs (puisque Q = C.V)
-----
3)
V1 = V2 + R.i
V1 = (K - C1V1)/C2 + R.i
V1 = (K - C1V1)/C2 - R.C1.dV1/dt
R.C1.dV1/dt + V1.(1 + C1/C2) = K/c2
R.C1.C2.dV1/dt + V1.(C2 + C1) = K
(R.C1.C2/(C1+C2)).dV1/dt + V1 = K/(C1+C2)
(R.C1.C2/(C1+C2)).dV1/dt + V1 = (C1.V10 + C2.V20)/(C1+C2)
Tau = R.C1.C2/(C1+C2) et A1 = (C1.V10 + C2.V20)/(C1+C2)
-----
Sauf distraction. 




