Inscription / Connexion Nouveau Sujet
Circuit en régime sinusoïdal
Bonjour, voilà j'ai besoin d'aide pour résoudre ce problème en électricité :
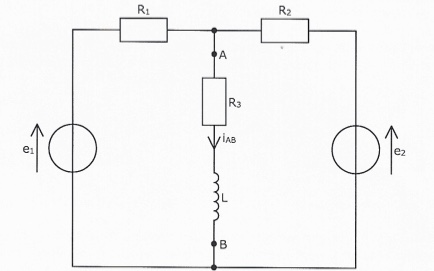
R1=0,1Ω, R2=0,2Ω, R3=30Ω
L=0,1H, f=50hz
e1=E1√2 cos(wt), e2=E2√2 cos(wt), E2 reste à déterminer et e2 a la même pulsation que e1
On considère le circuit en régime sinusoïdal forcé
A u(t)=U√2 cos(wt+φ) on associe le complexe u=U√2 e^j(wt+φ)= U e^jwt
- exprimer IAB la valeur efficace de iAB
- on veut que le dipôle AB constitué de R3 et L absorbe la puissance PAB=850W
Calculer la valeur de E2 et la valeur efficace de la fém e2
- calculer alors UAB la valeur efficace de uAB
Bonsoir
Plusieurs méthodes sont ici possibles.
La plus rapide consiste sans doute à appliquer le théorème de Millman pour obtenir l'expression de la tension complexe uAB.
Si ce théorème n'est pas à ton programme, tu peux commencer par simplifier le circuit en remplaçant les deux branches (e1,R1) et (e2,R2) par une seule branche équivalente correspondant à l'association en série d'un générateur de fém "e" et d'une résistance R. Cela peut se faire en appliquant la méthode dite de "la transformation Thévenin - Norton". On obtient le même résultat en appliquant le théorème de Thévenin mais ce théorème a disparu de nombreux programmes...
Je te laisse réfléchir et proposer une solution.
Si je me place dans le circuit complexe:
Je remplace R1 par Z1, R2 par Z2 et R3 avec L par Zp (Zp=R3+jwL)
Alors UAB=Zp * IAB
D'où IAB=UAB/Zp
Or d'après Milleman:
UAB= (E1/Z1 + 0 + E2/Z2) / (1/Z1 + 1/Z2 + 1/Zp)
Est ce bien cela?
J'ai peur de m'être embrouillée avec les notations complexes et les réels...
Bonjour
Ton application du théorème de Millman est correcte. Je retiens ta notation Zp pour l'impédance complexe du dipôle branché entre A et B. En revanche, puisque l'impédance complexe d'un conducteur ohmique est égale à sa résistance, autant garder les notations R1 et R2 . En soulignant les grandeurs complexes, cela donne :
La simplification d'écriture est obtenue en multipliant tous les termes par le produit des deux résistances. Pour l'intensité du courant à travers la branche (AB) :
Je te laisse continuer...
J'ai peur de m'être embrouillée avec les notations complexes et les réels...
Je ne connais pas exactement ton niveau. Peut-être le document ci-dessous (parties 1 et 3) pourra-t-il t'aider...
Toutefois, n'y a-t-il pas un autre moyen de résoudre ce problème sans utiliser uABen premier lieu car c'est dans la question 3 qu'on nous demande de trouver UAB
J'ai trouvé finalement:
IAB = (R2E1+R1E2) / (R1.R2 + (R3+ZL)(R2+R1))
D'où le module IAB=(R2E1 + R1E2) / (√(R1R2 + R2R3 +R1R3)^2 + ((R1+R2)Lw)^2)
Est ce bien ce qu'il fallait trouver?
la question 3 demande de calculer la valeur numérique UAB dans le cas particulier PAB=850W.
À mon avis, cela n'interdit pas de faire intervenir la valeur littérale complexe uAB comme intermédiaire dans le raisonnement.
Ton résultat est correct. Facile alors d'obtenir la puissance moyenne (ou puissance active) PAB.
Alors PAB=UAB*IAB?
Revois bien ton cours sur la notion de puissance moyenne. Éventuellement, le document dont je t'ai fournie la référence pourra t'aider.
L'ex pression la plus générale est :
PAB=UAB.IAB.cos(
)
où
désigne le déphasage entre les valeurs instantanées iAB et uAB. Heureusement : il y a plus simple ici : la puissance moyenne est la somme des puissances moyennes reçues par les différents dipôles de la branche (AB) :
PAB = PR3 + PL
Il se trouve qu'une inductance ne consomme pas de puissance en moyenne : PL = 0 .
Puisqu'une résistance ne produit pas de déphasage entre tension à ses bornes et intensité, on obtient simplement :
PAB = PR3 =R3.I2AB (résistance par carré de la'intensité efficace)
Il est très facile de déduire I2AB de la valeur complexe associée à iAB ...
L'impédance d'un conducteur ohmique est égale à sa résistance, donc , en valeurs efficaces :
UAB = R3.IAB
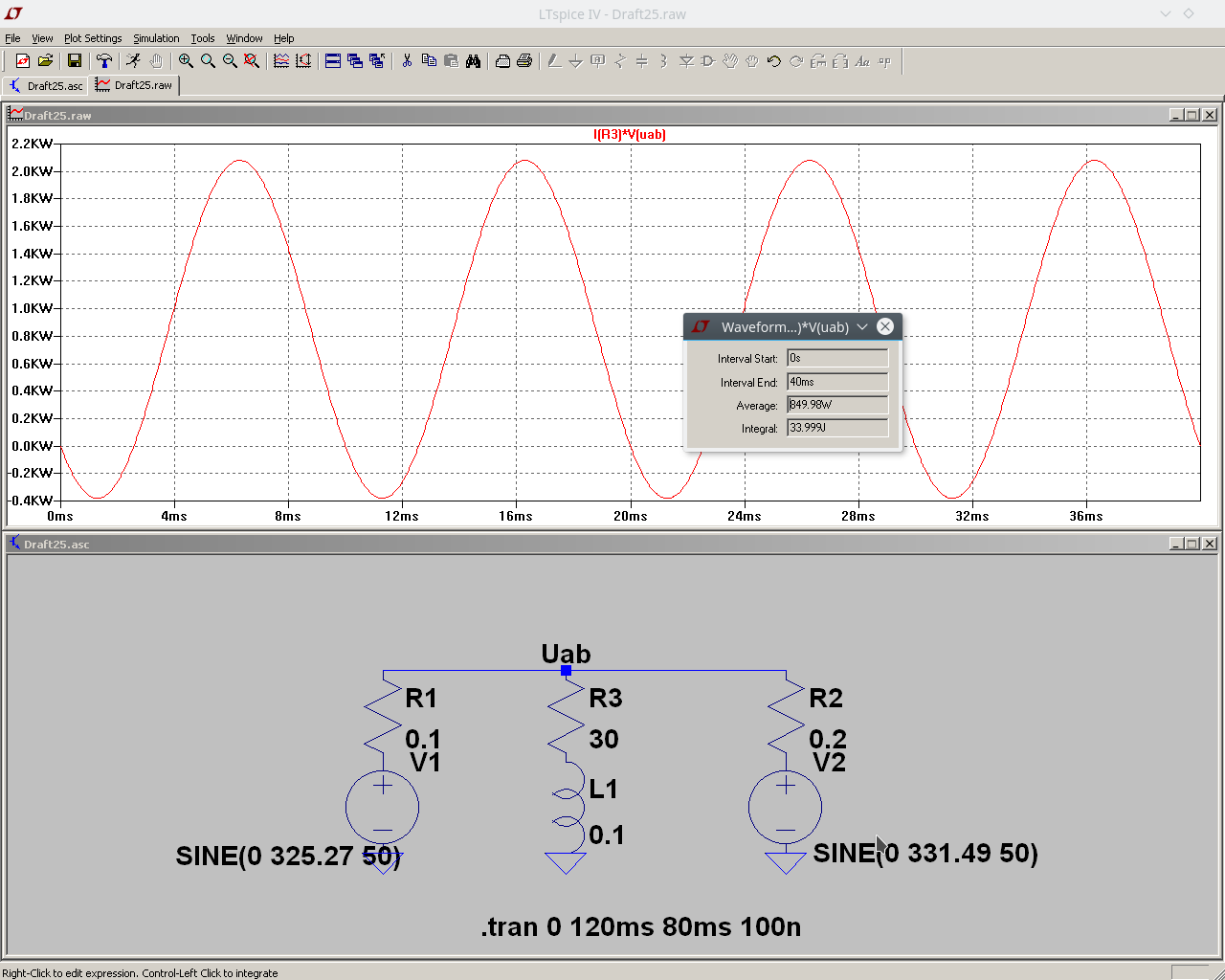
Pour le logiciel : j'ai utilisé LTspice : logiciel gratuit téléchargeable. On trouve sur le net de nombreuses fiches sur son utilisation. On dessine le circuit, on entre les valeurs des composants, on définit les générateurs : tension continue nulle, amplitude (230
2 et 2342) phase initiale nulle. On fait apparaître la courbe représentant les variations en fonction du temps de la puissance instantanée sur une durée multiple de la période. On obtient une sinusoïde de période T/2 = 10ms ; le logiciel calcule alors la valeur moyenne de cette puissance.
Attention : la valeur moyenne de la puissance doit nécessairement se calculer sur une période ou sur un nombre entier de périodes (ici 40ms). Voici ci-dessous une copie d'écran du résultat.
Annuler
connectez vous