Inscription / Connexion Nouveau Sujet
Circuit électrique
Bonjour,
j'ai deja posé plusieurs questions hier relatives à un circuit électrique et me voilà confronté à l'étude d'un autre circuit.
J'ai trouvé la relation qui lie Ve à Vs dans le domaine temporel:
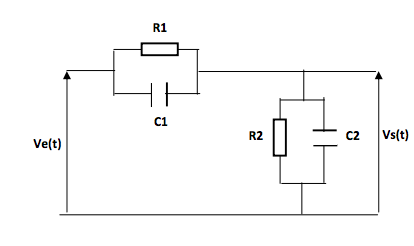
(R2/(R1+R2))Ve + ((R1R2)/(R1+R2))C1.dVe/dt = Vs + ((R1.R2)/(R1+R2)).(c1+c2).dVs/dt
Il m'est ensuite demandé d'établir une relation entre R1, C1, R2 et C2 de telle sorte que Vs(t) = k.Ve(t)
J'imagine je dois trouver cette relations à partir l'équation:
((R1R2)/(R1+R2))C1.dVe/dt = ((R1.R2)/(R1+R2)).(c1+c2).dVs/dt.Vs mais je ne suis pas certain étant donné que ça me donne à la fin une relation un peu compliquée. 
Suis-je sur la bonne piste ?
Merci d'avance, 
Bonjour gbm,
Je ne trouve malheureusement pas dans ton lien une réponse à ma question ...
Merci quand même et bon réveillon à toi aussi ! 
Dans la théorie du moindre effort...  tu pourrais simplifier ton équation (R2/(R1+R2))Ve + ((R1R2)/(R1+R2))C1.dVe/dt = Vs + ((R1.R2)/(R1+R2)).(c1+c2).dVs/dt : ce que je ferais, c'est que j'imposerais ve de telle sorte que dve/dt soit nul (si tu vois ce que je veux dire).
tu pourrais simplifier ton équation (R2/(R1+R2))Ve + ((R1R2)/(R1+R2))C1.dVe/dt = Vs + ((R1.R2)/(R1+R2)).(c1+c2).dVs/dt : ce que je ferais, c'est que j'imposerais ve de telle sorte que dve/dt soit nul (si tu vois ce que je veux dire).
Tu obtiens un truc qui ressemblera à peu près à k Ve (t) = Vs (t), à toi de déterminer les conditions pour que ça soit exactement de la même forme.
Joyeux Noël
Bonjour electro,
J'ai pas compris ce que t'as fait. Tu pourrais m'expliquer plus clairement stp
Merci et joyeux Noël à toi aussi !
Etablir une relation entre R1, C1, R2 et C2 de telle sorte que Vs(t) = k.Ve(t)
R // C :
Z = (R/(jwC))/(R + 1/(jwC)) = R/(1+jwRC)
----
Vs/(R2/(1+jwR2C2)) = Ve/(R1/(1+jwR1C1) + R2/(1+jwR2C2))
Vs/R2 = Ve.(1+jwR1C1)/(R1.(1+jwR2C2) + R2.(1+jwR1C1))
Vs/Ve = R2 * (1+jwR1C1)/(R1.(1+jwR2C2) + R2.(1+jwR1C1))
et si R1C1 = R2C2, alors :
Vs/Ve = R2 * (1+jwR1C1)/(R1+R2).(1+jwR1C1))
Vs/Ve = R2/(R1+R2)
Vs = k.Ve avec k = R2/(R1+R2) à la condition que R1C1 = R2C2
-----
Sauf distraction. 
Bonjour J-P je ne comprends pas comment tu passes de la ligne où tu exprimes Z à la ligne où tu as dans ton équation Ve et Vs. Pourrais tu s'il te plait détailler un peu plus ton calcul? Merci d'avance.
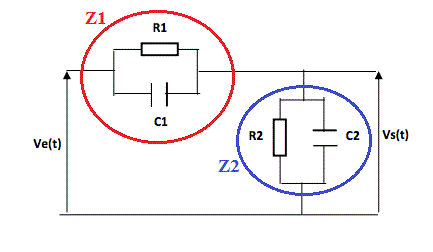
Diviseur de tension qui donne directement :
Vs/Z2 = Ve/(Z1 + Z2)
Vs/Ve = Z2/(Z1+Z2) (1)
Or un C en // sur R a une impédance Z = R/(1+jwRC)
Donc Z1 = R1/(1+jwR1C1)
et Z2 = R2/(1+jwR2C2)
Cela remis dans (1) -->
Vs/Ve = (R2/(1+jwR2C2))/(R1/(1+jwR1C1) + R2/(1+jwR2C2))
-----
Sauf distraction. 
Merci beaucoup J-P je n'avais pas pensé à appliquer le diviseur de tension aux ensembles Z1 et Z2.
Bonne fin de semaine !
Je travaille aussi sur le même exercice et rencontre quelques difficultés. Je suis parvenu jusqu'à l'avant dernière question, mais je suis confronté à un problème : on me demande de déterminer le déphasage antre Vs et Ve avec R1 = 9 kohm, R2 = 1 kohm, C2 = 10 nF et les trois valeurs de C1 suivantes : C1 = 220 pF, C1 = 111 pF et C1 = 56 pF. Seulement pour calculer le déphasage, je dois avoir l'argument de Z, et pour avoir Z, je dois avoir sa partie réelle R (résistance) et sa partie imaginaire X (condensateur). Or pour calculer X (la réactance) à partir des données de la question, j'ai besoin de la fréquence du courant (Xc = 1/cw ; avec w = 2πf). Et là est le problème : je n'ai pas la fréquence du courant pour le système électrique étudié.
Suis-je sur la bonne voie ou y a-t-il un autre moyen de calculer la réactance du condensateur ?
Merci d'avance 
J'oubliais : la question précédente était de tracer la réponse pour ces mêmes données. Je ne sais pas si cela peut aider pour cette question ou non...
Sauf cas particulier (par exemple ici pour R1C1 = R2C2), le déphasage de Vs/Ve dépend bien de w.
On peut le donner par Phi = fonction de w.
Vs/Ve = (R2/(1+jwR2C2))/(R1/(1+jwR1C1) + R2/(1+jwR2C2))
Vs/Ve = R2 * (1+jwR1C1))/(R1(1+jwR2C2) + R2.(1+jwR1C1))
Vs/Ve = R2 * (1+jwR1C1))/(R1 + R2 + jwR1R2(C1+C2))
Vs/Ve = (R2/(R1+R2)) * (1+jwR1C1))/(1 + jwR1R2(C1+C2)/(R1+R2))
Phi = arctan(wR1C1) - arctan(wR1R2(C1+C2)/(R1+R2))
Aux erreurs de calcul près :
Vs/Ve = (R2/(1+jwR2C2))/(R1/(1+jwR1C1) + R2/(1+jwR2C2))
Vs/Ve = R2 * (1+jwR1C1))/(R1(1+jwR2C2) + R2.(1+jwR1C1))
Vs/Ve = R2 * (1+jwR1C1))/(R1 + R2 + jwR1R2(C1+C2))
Vs/Ve = (R2/(R1+R2)) * (1+jwR1C1))/(1 + jwR1R2(C1+C2)/(R1+R2))
Phi = arctan(wR1C1) - arctan(wR1R2(C1+C2)/(R1+R2))
qu'on peut encore "triturer" par la relation arctan(a) - arctan(b) = arctan((a-b)/(1 + ab)) (A vérifier)
On arrive alors à :
Phi = w.R1(R1C1 - R2C2)/(R1+R2 + w²R1²R2C1(C1+C2))
Calculs non vérifiés.

Bonsoir J-P
Si on devait tirer une conclusion de ce résultat en fonction des trois valeurs de C1, qu'est-ce-que ce serait?
Sous cette forme, j'ai du mal à voir comment changerait le déphasage en fonction de C1...
Merci d'avance
Attention, il manque au moins un arctan() dans la dernière ligne de ma réponse précédente ... aux autres erreurs près.

Sans correction des erreurs éventuelles, on arrive à ceci :
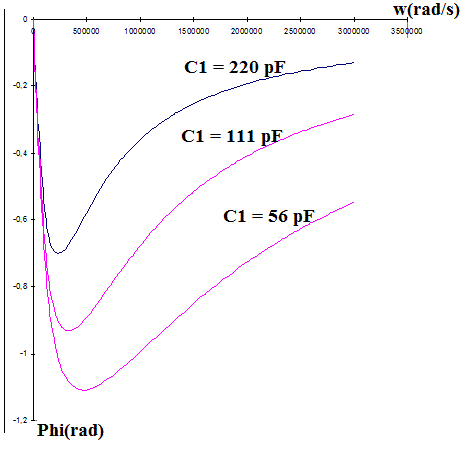
Si on veut des diagrammes de Bode (pour la phase), alors, on doit prendre une échelle logarithmique sur l'axe des w. (et pas une échelle linéaire comme je l'ai fait)



