Inscription / Connexion Nouveau Sujet
Circuit avec AOP comment appliquer la loi des mailles?
Bonsoir,
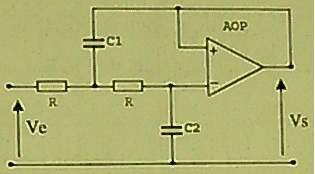
j'aurai besoin d'aide pour démarrer cet exercice d'électronique(schéma en bas, et les mailles que je considère)en utilisant les lois des mailles et des nœuds comme mon prof(pas Millman),le voici:
Dans le montage suivant l'amplificateur opérationnel est supposé idéal et en régime sinusoïdale.
Montrer que l'expression générale de la fonction de transfert est:
s'écrit:
2)Donner les expressions de et
3)Quel est le type est l'ordre du filtre?
J'ai pas mit toute les questions pour l'instant,il faut traçer des diagrammes,mais j'aurai surtout besoin d'aide pour les questions 1 et 2 pour l'instant.
Voici ce que j'ai pu dire pour la 1:
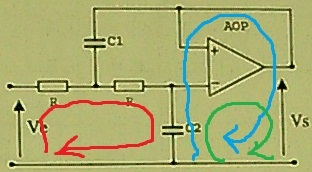
1)J'utilise la boucle rouge pour trouver ,et selon cela
,si les résistances sont en séries.
Ensuite la boucle bleu donne ,mais si c'est la boucle verte qu'il faut prendre pour calculer
on a
Avec
donc
...
étant le courant d'entré.
Mais ce que j'ai écris pour la loi des mailles est-ce vrai?
Et si on réfléchissait quelques secondes.
Qu'aurait-on avec w = 0 (tension constante continue), par exemple Ve = 1 Volt continu constant.
Si je fais w = 0 dans l'expression que tu donnes de T(jw), on trouve : T(w=0) = 1/(1+0+0) = 1
Or, avec w = 0, un condensateur (en régime établi) se comporte comme un circuit ouvert.
Le schéma (avec w = 0) est donc équivalent à :
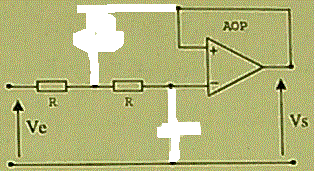
Avec + 1 Volt continu à l'entrée Ve, Vs file à Vsaturation et y reste ... soit en positif, soit en négatif car la réaction se fait sur l'entrée V+
Ce qui n'est pas du tout ce qui est annoncé.
Ce montage ne travaille pas en mode linéaire...
C'est foireux.
Sauf distraction. 
Oui, les entrées + et - sont inversées (une erreur sans doute)...
En inversant les entrées + et - , on a un filtre passe-bas de type Sallen-Kay qui correspond bien au proposé.
Les équations des mailles et des noeuds sont les suivantes :
On peut aussi ajouter :
(ampli op parfait)
en inversant les entrées + et -
Il suffit de résoudre ce système pour trouver la fonction de transfert.
Ce pauvre jean469 n'a vraiment pas de chance ; ce n'est pas la première fois que son professeur fait preuve d'incompétence en posant des problèmes incohérents sur le plan scientifique. Je pense en particulier à l'électrostatique mais ici : c'est encore plus gros !
Bonjour,
Quelques explications à propos de la sévérité de mon message d'hier soir.
La première séance de travaux pratiques sur l'ampli. op. au niveau (bac+1) consiste à présenter les différents modes de fonctionnement de l'ampli. op. et en particulier à montrer expérimentalement que, dans les cas simples où la sortie n'est reliée qu'à une seule entrée par résistance :
- le régime linéaire est impossible si l'entrée concernée est l'entrée non inverseuse E+ ; dans ces cas, soit l'ampli op se bloque en saturation haute ou basse, soit il fonctionne en comparateur ;
- le régime linéaire est possible si l'entrée concernée est l'entrée non inverseuse E- ; j'écris possible, pas obligatoire : la tension d'entrée peut être de trop grande amplitude, la fréquence peut être trop élevée, la sortie peut saturer en courant... etc...
Bref : tout étudiant et a fortiori tout professeur, d'un simple coup d'œil sur le schéma proposé ici, doit être capable d'affirmer que le montage proposé ne peut fonctionner en régime linéaire.
Puisque l'étude rigoureuse des systèmes bouclés est reportée aux niveau (bac+3) ou (bac+4) depuis le milieu des années 90, au niveau licence ou classes prépas, en cas de montage comportant une liaison par résistance S - (E+) et une liaison par résistance S -( E-), le concepteur du problème a deux choix :
1° : indiquer le type de fonctionnement de l'ampli. op. en demandant aux étudiants d'admettre ce résultat ;
2° : amener les étudiants à démontrer le résultat par une suite de questions très détaillées et de difficultés graduées...
Bien sûr, personne n'est à l'abri d'une étourderie (je suis bien placé pour le savoir
) mais ce professeur a déjà posé plusieurs problèmes incohérents cette année, ce qui est toujours déstabilisant pour les étudiants...
Je suis bien d'accord. Le minimum, pour un prof, est de faire attention à ne pas proposer des énoncés avec des erreurs grossières mais, effectivement, personne n'est à l'abri d'une erreur....
Jean469 a dû être rebuté par nos réponses parce qu'il n'est pas revenu...
Bonjour les gars,non j'ai pas été rebuté,juste étonné,moi même je viens de voir l'erreur!
Le pire c'est que c'est un autre prof encore vanoise,en gros je dois avoir 3 prof dont on m'a déjà dit qu'ils sont soit mauvais,soit leurs énoncés sont insensés.
Là ça montre du laisser aller de la par de ma fac...
J'ai plusieurs profs de physique,j'espère que les autres sont bons...
En tout cas merci pour votre aide vanoise,J-P et Aragorn.
Je vais réfléchir à la suite de l'exo maintenant mais ça reste hallucinant...
Bonjour !
Alors,en reprenant les calculs de Aragorn(merci au passage),j'ai obtenue:
Après ce que je trouve ne ressemble pas à ce qui est demander,il faut savoir par quoi on divise le numérateur et le dénominateur pour avoir 1 au numérateur.
Ensuite dans ce type d'exo,un de mes prof exprimait Vs et Ve en fonction de ie(courant d'entré) et appelait tous les condensateurs C et les résistances R,mais pas sûr qu'on puisse faire ça pour cet exo...
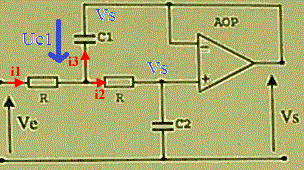
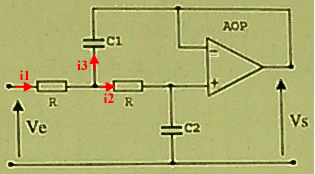
Ve - R.i1 - R.i2 - Vs = 0
i2 = C2.jw.Vs
i1 = i2 + i3
Ve - R.i1 - Uc1 = Vs
i3 = jwC1.Uc1
On élimine i3 :
Ve - R.i1 - R.i2 - Vs = 0
i2 = C2.jw.Vs
i1 = i2 + jwC1.Uc1
Ve - R.i1 - Uc1 = Vs
On élimine i2 :
Ve - R.i1 - R.C2.jw.Vs - Vs = 0
i1 = C2.jw.Vs + jwC1.Uc1
Ve - R.i1 - Uc1 = Vs
On élimine i1 :
Ve - R.(C2.jw.Vs + jwC1.Uc1) - R.C2.jw.Vs - Vs = 0
Ve - R.(C2.jw.Vs + jwC1.Uc1) - Uc1 = Vs
Ve - 2.R.C2.jw.Vs - jw.R.C1.Uc1 - Vs = 0
Ve - R.C2.jw.Vs - Uc1.(1+jwRc1) = Vs
Uc1 = (Ve - 2.R.C2.jw.Vs - Vs)/(jw.R.C1)
Uc1 = (Ve - R.C2.jw.Vs - Vs)/(1+jwRc1)
(Ve - 2.R.C2.jw.Vs - Vs)/(jw.R.C1) = (Ve - R.C2.jw.Vs - Vs)/(1+jwRc1)
(Ve - 2.R.C2.jw.Vs - Vs).(1+jwRc1) = jwRC1.(Ve - R.C2.jw.Vs - Vs)
Ve.(1+jwRC1-jwRC1) = -Vs(j²w²R²C1C2 + jwRC1 - (1 + jwRC1)(2RC2jw+1))
Ve.(1+jwRC1-jwRC1) = -Vs(j²w²R²C1C2 + jwRC1 - 2RC2jw - 1 - 2j²w²R²C1C2 - jwRC1)
Ve = -Vs(- 2RC2jw - 1 - j²w²R²C1C2)
Vs/Ve = 1/(1 + 2jwRC2 + j²w²R²C1C2)
A comparer avec Vs/Vz = 1/(1 + 2a.jw/wo + (jw/wo)²
--> wo² = 1/(R²C1C2)
wo = 1/(R*RacineCarrée(C1C2))
a/wo = RC2
a = R.C2/(R*RacineCarrée(C1C2))
a = RacineCarrée(C2/C1)
Sauf distraction (pas vérifié).
Bonsoir,
Excellent travail de JP puisque ton professeur exige la loi des mailles et la loi des nœuds. Mais tout de même : ton professeur est un peu sadique !
Première ligne : le théorème de Millman donne une expression de VN en fonction de Ve et VS ;
deuxième ligne : en absence de courant d'entrée par (E+) l'ensemble {R,C2} se comporte en diviseur de tension : cela donne une relation entre VN et VS ;
troisième ligne : élimination de VN entre les deux relations précédentes: on obtient une relation entre Ve et VS.
quatrième ligne : on simplifie la relation précédente en faisant apparaître le rapport VS/Ve et c'est fini en ce qui concerne l'expression de T !
Sans parler du temps passé, la probabilité, pour un étudiant encore peu expérimenté, de se tromper dans les signes et les calculs n'est manifestement pas la même !
Bonjour,
Ensuite dans ce type d'exo,un de mes prof exprimait Vs et Ve en fonction de ie(courant d'entré) et appelait tous les condensateurs C et les résistances R,mais pas sûr qu'on puisse faire ça pour cet exo...
Poser C1 = C2 retirerait beaucoup d'intérêt à ce problème. En effet, comme l'a montré JP, la valeur de
dépend du rapport C2/C1. Or, comme tu vas sans doute être amené à le montrer par la suite, l'allure du diagramme de Bode de ce Passe-Bas du second ordre dépend fortement de la valeur de , en particulier du signe de (22-1).[
Sauf distraction (pas vérifié).
Merci beaucoup J-P pour ton aide et ces explications détaillées!!!
Bonsoir,
Mais tout de même : ton professeur est un peu sadique !
Première ligne : le théorème de Millman donne une expression de VN en fonction de Ve et VS ;
Oui assez sadique ce prof!
Mais c'est quoi VN?
Poser C1 = C2 retirerait beaucoup d'intérêt à ce problème.
Ah ok!
Après si mon prof me demande de retraité ça en Millman je le ferai,ça sera plus simple d'ailleurs.
Oui, enfin Millman plus simple ... reste à voir.
J'ai extrêmement détaillé ma réponse avec les lois des mailles et des noeuds, mais on peut très aisément faire plus "direct" par cette méthode, par exemple ainsi :
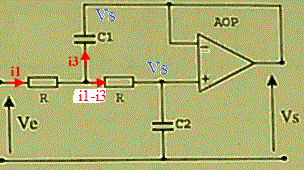
Ve - R.i1 - R(i1-i3) - Vs = 0
i1-i3 = jwC2.Vs
Ve - R.i1 - i3/(jwC1) - Vs = 0
Ve - R.i1 - jwRC2.Vs - Vs = 0 --> i1 = (Ve - jwRC2.Vs - Vs)/R
Ve - R.i1 - (i1 - jwC2.Vs)/(jwC1) - Vs = 0
Ve - R.(Ve - jwRC2.Vs - Vs)/R - [(Ve - jwRC2.Vs - Vs)/R - jwC2.Vs]/(jwC1) - Vs = 0
Ve - Ve + jwRC2.Vs + Vs - Ve/(jwRC1) + (C2/C1).Vs + Vs/(jwRC1) + (C2/C1).Vs - Vs = 0
[jwRC2.Vs + Vs + (C2/C1).Vs + Vs/(jwRC1) + (C2/C1).Vs - Vs].jwRC1 = Ve
Vs.(j²w²R²C1C2 + 2jwRC2 + 1) = Ve
Vs/Ve = 1/(1 + 2jwRC2 + j²w²R²C1C2)
*****
Et voila.
Ne pas penser que je suis anti Millman ... néanmoins, le porter au pinacle comparé aux autres techniques me parait très largement exagéré.
Oui, enfin Millman plus simple ... reste à voir.
Ne pas penser que je suis anti Millman ... néanmoins, le porter au pinacle...
Oui effectivement,on fait souvent l'éloge de cette méthode!
Mais c'est quoi VN?
Le point N est pour moi le nœud entre les deux résistances.
Ok merci vanoise
Bonsoir,
Ok merci vanoise
De rien ! Je crois qu'il y a une méthode pour respecter les consignes de ton professeur tout en évitant la principale difficulté liée à l'application des lois de Kirchoff : l'élimination des trois variables intermédiaires i1,i2,i3 ; apparemment tu n'y étais pas arrivé tout seul mais rassure-toi : il y a bien peu d'étudiants capable de s'en sortir en un temps raisonnable, le jour d'un concours ou d'un examen : j'ai été payé suffisamment longtemps comme membre de jury de concours nationaux niveaux (bac+2) à (bac+4) pour le savoir !
Voici une méthode pour n'avoir qu'une seule variable intermédiaire à éliminer : vN :
Étape n° 1 : puisqu'une intensité est un quotient (tension/impédance), la loi des noeuds telle qu'elle a déjà été écrite devient :
Soit après multiplication de tous les termes par R et simplification :
Étape n°2 : diviseur de tension comme déjà expliqué qui permet d'obtenir une nouvelle relation entre vN et vS.
Étape n° 3 : élimination de la seule variable intermédiaire vN entre les deux relations précédentes.
Étape n° 4 : simplification et mise en forme du rapport vS/vE.
Ainsi, tu n'as pas utilisé le théorème de Millman et tu tombes sur un problème avec une seule et non trois variable intermédiaire à éliminer. Cela est beaucoup plus facile !
Annuler
connectez vous