Bonjour
court-circuité : remplacer le dipôle par un fil conducteur de résistance négligeable.

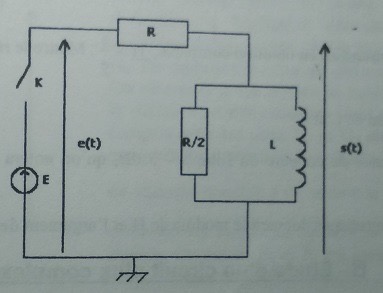
Mais on a un court-circuit dans quels cas ? Comment savoir que l'on est en présence d'un court-circuit ?
Et ça a quelles conséquences ?
Merci beaucoup.

La tension aux bornes de l'inductance est égale, dans le cas général, à .
Dans le cas particulier du régime continu, la dérivée est nulle à chaque instant, donc u_L = 0 à chaque instant et cela quelle que soit l'intensité du courant continu qui circule dans l'inductance. L'inductance a donc, dans ce cas particulier, exactement les même propriétés qu'un fil conducteur de résistance négligeable. Pour étudier le circuit en régime continu, tu peux donc enlever l'inductance et la remplacer par un fil conducteur de résistance négligeable. Cette opération s'appelle "court-circuiter" l'inductance. Les calculs deviennent alors beaucoup plus simples.

Merci beaucoup pour cette clarification.
Et du coup en régime continu donc lorsque la bobine est court-circuitée, est-ce que l'on a équivalence entre les deux circuits que j'ai dessiné en dessous ?
Peut-on simplifier le circuit comme je l'ai fait à droite du symbole « équivalent » ?

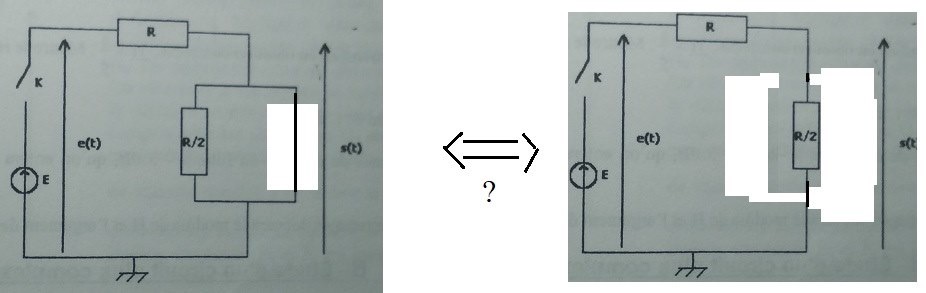
D'accord avec ton schéma équivalent de gauche mais pas avec celui de droite. La tension s est commune à (R/2) et au court-circuit et vaut zéro. Selon la loi d'Ohm : (R/2) n'est parcouru par aucun courant, on peut donc aussi l'enlever ; le courant passe entièrement à travers le fil de résistance négligeable. L'essentiel à retenir : s=0 dans ce cas particulier.

PS : tu peux aussi,si cela te rassure, calculer la résistance équivalente à la mise en parallèle d'une résistance (R/2) et d'une résistance nulle. Tu vas trouver zéro !

Désormais, y a-t-il bien équivalence avec le circuit à droite ?
Pas sûr d'avoir compris pourquoi on n'avait pas équivalence dans mon image précédente...
Et comment pourrait-on calculer la résistance équivalente car on aurait, pour des résistances en parallèle : [tex]\frac{1}{R_{eq}}=\frac{1}{R/2}+\frac{1}{0}[\tex]
Un dénominateur nul ?!
Et je ne comprends pas pourquoi vous invoquez la loi d'Ohm...

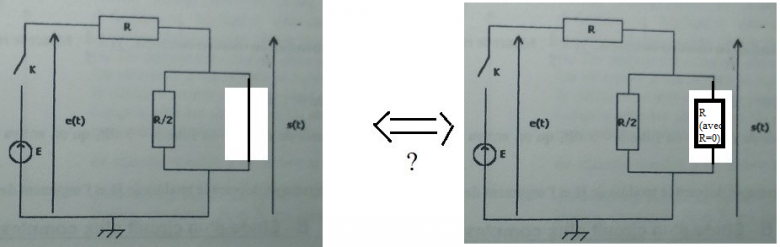
Si tu appliques la loi d'Ohm à R/2 :
s=(R/2).I' = 0
La valeur "zéro" est imposée par le fil de résistance négligeable. Puisque R0, l'intensité du courant I' à travers R/2 est nécessairement I'=0. Puisque cette résistance n'est parcourue par aucun courant, il est possible de l'enlever sans perturber le fonctionnement du reste du circuit, d'où le schéma équivalent ci-dessous. Simple, non ?
Sinon, soit deux résistances en parallèles :



Suppose : R₁=0 ; R₂ 0 ; l'égalité précédente conduit bien à R_e=0.

Merci beaucoup, je crois que je comprends beaucoup mieux !

C'est classique dans les sujets de concours (je suis en deuxième année de prépa) ce type de court-circuit ou pas ?

Et est-ce qu'on a bien équivalence entre les deux circuits en-dessous ?

Oui compte tenue de la relation donnant la résistance équivalente avec une des résistance nulle.

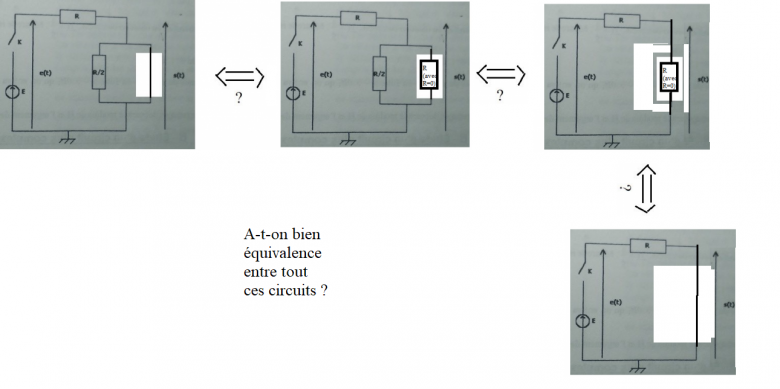
Donc absolument tous les schémas sont équivalents ?
Et ça arrive souvent dans les sujets de concours ce genre de court-circuit ?

Oui ! avec l'autre cas classique où le dipôle est équivalent à un interrupteur ouvert, ce qui conduit à une intensité nulle dans la branche à laquelle il appartient. Cas d'un condensateur en régime continu par exemple.

OK, merci !
Et dans le cas que vous décrivez, "où le dipôle est équivalent à un interrupteur ouvert, ce qui conduit à une intensité nulle dans la branche à laquelle il appartient. Cas d'un condensateur en régime continu par exemple." : auriez-vous un exemple de circuit s'il vous plait ?
Je n'en trouve pas du tout...

Dans le circuit étudié ici, remplace L par  C et pose toi la question de la valeur de s interrupteur K fermé en régime permanent.

Dans le cas que vous décrivez on aura aussi un court-circuit ?

Relis mes précédents messages : il faut montrer que, dans ce cas, C est équivalent à un interrupteur ouvert.  Quel est l'expression de  i dans une branche contenant C ? Que devient la relation en régime permanent  ?

Dans une branche contenant C, en régime permanent, i devient nul.
Mais quelles sont donc les conséquences sur le circuit ?

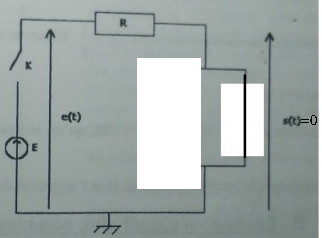
Dans le cas où o remplace L par un condensateur, on a en régime permanent, C équivalent à un interrupteur ouvert.
Dans ce cas a-t-on équivalence entre les 2 circuits ci-dessus ?
Que vaut donc s(t) ?
Merci.

Notion de diviseur de tension.

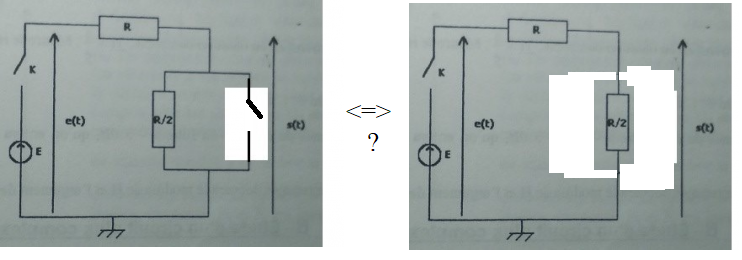
Mais est-ce que les schémas de mon message de 14h35 sont corrects ?
Et je n'ai toujours pas trouvé l'expression de s(t)......

Montage équivalent correct.
Diviseur de tension : tu trouveras la démonstration générale ici : Résultat à retenir absolument : il s'agit de très loin du résultat le plus souvent utilisé en électronique.
Sinon, tu peux t'en sortir à l'aide de la loi d'Ohm :
E=(R+R/2).I
s=(R/2).I
Par substitution ou division membre à membre :
s=E/3