Inscription / Connexion Nouveau Sujet
cinematrique
bonjour de l'aide svp
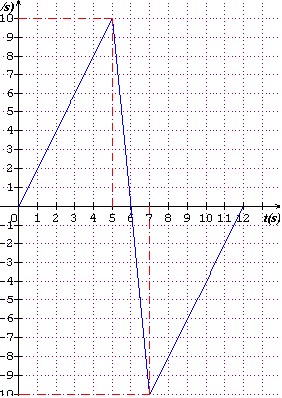
la representation graphique de la vitesse v=f(t) d'un mobile est donnée par la figure suivante: (voir figure)
1)calculer les accelerations du mobile au cours des trois phases du mouvement.
2)tracer la representation graphique a=g(t) de l'acceleration a en fonction du temps.
3)calculer l'espace parcouru par le mobile.
je precise que v=f(t) est en bleu(sans pointillets).ce qui est en rouge(avec pointillets) c'est pour indiquer les 3 phases du mouvement
merci de m'aider
Salut 111111
L'accélération d'un mobile à un instant t c'est la valeur de la dérivée de sa vitesse, autrement dit le coefficient directeur de la tangente à la vitesse.
Sur [0;5], g'(t)=2
a toi 
La valeur de l'accélération, c'est la dérivée de la vitesse ok ?
Soit f une fonction dérivable en
Un nombre dérivé (genre ) c'est quoi en fait ? C'est le coefficient directeur de la tangente à
au point
ok ?

Cool 
Sur ton graphe, tu as la représentation de la vitesse. On voit qu'on peut découper ce graphe en 3 tronçons.
Sur [0;5], quel est le coefficient directeur de la droite ?
On pose A(0,0) et B(5,10)
le coefficient directeur est soit
(quand on augmente de 1 par la droite, on monte de 2 carreaux)
On a donc sur [0;5] a(t)=2.
Sur [5;7] a(t)=... ?

Ton graphe représentant a(t) est discontinu en 5 et en 7.
3° Essaie de calculer la distance totale (v=d/t, et prends des valeurs de vitesse moyennes : sur [5;7] la vitesse est en moyenne de 5m/s)

Bonne nuit
Phase 1:
La vitesse passe linéairement de 0 à 10 m/s en 5 s :
a1 = (10-0)/5 = 2 m/s²
phase 2:
La vitesse passe de manière régulière de +10 m/s à -10 m/s en 2 s :
a2 = (-10-(+10))/2 = - 10 m/s²
phase 3:
La vitesse passe de manière régulière de -10 m/s à 0 m/s en 5 s :
a3 = (0-(-10))/5 = 2 m/s²
-----
phase 1
distance 1 = a1.(delta t)²/2 = 2 * 2² / 2 = 4 m
Les phases suivantes sont litigieuse, car une partie du trajet est dans un sens et une autre partie dans l'autre sens.
La question est-elle d'ajouter les valeurs absolues des distances parcourues ou bien de trouver l'écart de position entre le début et la fin de la phase.
Si c'est le cas, il faudrait savoir si les mouvement sont recrilignes et tous dans la même direction.




