Niveau licence

Cinématique : mouvement circulaire

Posté par
nico10310 23-03-17 à 17:30

Bonjour,
J'ai répondu à l'exercice ci-dessous et j'aimerai bien avoir une correction de mon travail et une aide pour la question 4. Merci

Énoncé :
Dans le référentiel R muni d'un repère orthonormé direct R(O,e_x, e_y, e_z) , un point P se déplace dans le plan z=0 sur une courbe définie par :
$\mathit{p}=Acos(phi)+Bsin(phi) \: et \: phi= wt \; avec \: \: phi \: appartient \: à \: [0,pi/2]$ A, B et w des constantes positives.

1) Donner l'expression des composantes du vecteur vitesse v_P/R dans la base cylindrique (e_p, e_phi, e_z) en fonction du temps. En déduire la nature du mouvement.

2) Donner l'expression des composantes du vecteur accélération a_P/R dans la base cylindrique (e_p, e_phi, e_z) en fonction du temps et de w.

3) Déterminer l'équation cartésienne de la trajectoire. Montrer que celle-ci est un cercle.

4) Déduire de la norme du vecteur a_P/R le rayon du cercle.

Mon travail :

Merci pour votre aide !

Posté par re : Cinématique : mouvement circulaire 23-03-17 à 22:24

Bonsoir
L'habitude sur ce site est d'écrire sa solution, sinon déchiffrer les scan de brouillons... Cela dit, je crois que tu as bien travaillé et je vais t'aider sur la question la plus difficile, celle concernant les caractéristiques de la trajectoire. Le reste est essentiellement du calcul.
En remarquant :

$x=\rho.\cos\left(\varphi\right)\quad;\quad y=\rho.\sin\left(\varphi\right)$
On peut écrire :

$\rho=A.\cos\left(\varphi\right)+B.\sin\left(\varphi\right)=A.\frac{x}{\rho}+B.\frac{y}{\rho}$
Donc :

$\rho^{2}=x^{2}+y^{2}=A.x+B.y$
D'où l'équation cartésienne de la trajectoire :

$x^{2}+y^{2}-A.x-B.y=0\quad ou\quad x.\left(x-A\right)+y.\left(y-B\right)=0$

L'équation générale d'un cercle de rayon R, ce centre C(xc,yc) est :

$\left(x-x_{C}\right)^{2}+\left(y-y_{C}\right)^{2}=R^{2}\quad ou\quad x^{2}+y^{2}-2x.x_{C}-2y.y_{C}=R^{2}-x_{C}^{2}-y_{C}^{2}$

Par identification, on constate que la trajectoire est un cercle de centre C( $\frac{A}{2}$ , $\frac{B}{2}$ ), de rayon :

$R=\frac{\sqrt{A^{2}+B^{2}}}{2}$

Ce cercle passe par les trois points de coordonnées : (0,0) ; (A,0) ; (0,B).

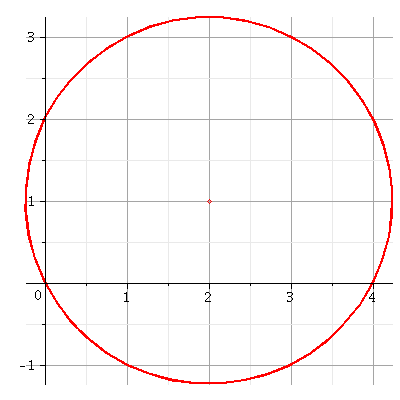
Voici en annexe le résultat obtenu pour A=4 et B=2 (unités non précisées...)

Cinématique : mouvement circulaire