Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Cinématique du solide indéformable

Posté par
TheBartov 18-10-13 à 23:54

Bonjour,

décidément la mécanique du solide ne me réussit pas. J'ai du mal, cette fois-ci, avec ce système là.

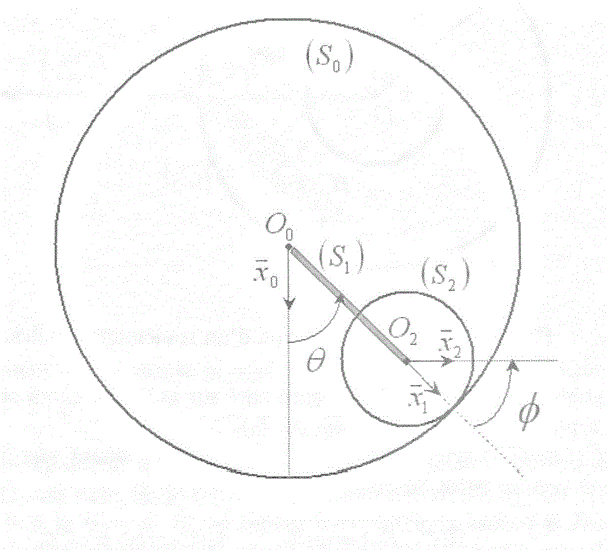
Annotation de la figure ci-dessous (tout en bas de la page):

\bullet (S_0) : Anneau de centre O_0, de rayon R, qui est fixe dans R_0(O_0,\vec{x_0},\vec{y_0},\vec{z_0})

\bullet (S_2) : Anneau de centre O_2, de rayon r, et le repère lié à l'anneau R_2(O_2,\vec{x_2},\vec{y_2},\vec{z_0})

\bullet (S_1) : Tige de longueur R-r liant O_2 et O_0, il porte le repère R_1(O_2,\vec{x_1},\vec{y_1},\vec{z_0})


PS : pour plus de commodités, je vais noter la base 1 sous cette forme : R_1(O_2,\vec{e_r},\vec{e_{\theta}},\vec{z_0})

On note

\large \left\lbrace\begin{array}l \theta=(\vec{x_0} ; \vec{e_r})\\ \phi=(\vec{e_r} ; \vec{x_2}) \end{array}

Note : "Pour faciliter les calculs, il est préférable de tout exprimer dans la base R_1"



Questions :

1)Calculer le vecteur \vec{\Omega}_{(S_2)/R_0}, rotation instantanée de (S_2) dans R_0.

2)Donner les conditions de non glissement du disque (S_2) dans l'anneau (S_0).

3)En intégrant la condition de Roulement Sans Glissement (RSG) trouver la relation qui relient les angles \theta et \phi t0 du mouvement sans glissement, sachant que pour t=0 : \theta(0)=\phi(0)=0 rad

4)Calculer l'accélération du point de contact I_2 appartenant à (S_2) entre le disque et l'anneau.



Mes pistes : (est-ce juste ?)

1)Comme le solide 2 a une vitesse angulaire dans R_1, et que R_1 a une vitesse angulaire dans R_0, on peut appliquer le théorème de Chasles dans le cas des vitesses angulaires :

\Large \vec{\Omega}_{(S_2/S_0)}=\vec{\Omega}_{(S_2/S_1)}+\vec{\Omega}_{(S_1/S_0)}=[\dot{\phi}+\dot{\theta}]\vec{z_0}



2)Il faut résoudre l'inéquation suivante :
On note I2(S2) et I0(S0); tels que I0 et I2 coïncident en un point I (point coïncidant).


\large \vec{V_g}_{(S_2/S_0)}\neq \vec{0} \\ \\ \Longleftrightarrow \vec{V}_{(I_2/R_0)}-\vect{V}_{(I_0/R_0)} \neq \vec{0} \\ \\ \Longleftrightarrow \vec{V}_{(I_2/R_0)} \neq \vec{0} \\ \\ \Longleftrightarrow \vec{V}_{(O_2/R_0)}+\vec{\Omega}_{(S_2/S_0)} \wedge \vec{O_2I_2} \neq \vec{0} \\ \\ \Longleftrightarrow (R-r)\dot{\theta} \vec{e_{\theta}}+[\dot{\phi}+\dot{\theta}]\vec{z_0} \wedge r\vec{e_r} \neq \vec{0} \\ \\ \Longleftrightarrow [(R-r)\dot{\theta}+(\dot{\phi}+\dot{\theta})r]\vec{e_{\theta}} \neq \vec{0} \\ \\ \Longleftrightarrow [R\dot{\theta}+r\dot{\phi}]\vec{e_{\theta}} \neq \vec{0} \\ \\ \\                             \Longrightarrow R\dot{\theta}+r\dot{\phi} \neq 0       (1)



3) La relation (1) ne doit pas être vérifiée dans le cas des RSG. Ainsi on doit résoudre :

\large \int R\dot{\theta}+r\dot{\phi} dt= \int 0 dt \\ \\ \Longleftrightarrow  r\phi(t)+R\theta(t)=Cst \\ \\ C.I.\Longleftrightarrow Cst=0 \\ \\ RSG\Longleftrightarrow r\phi(t)=-R\theta(t)  \forall t\ge 0

(cette relation me semble bizarre...)

4) On a calculé \vec{V_{g}}_{S2/S0}=\vec{V}_{I_2/R_0} :

\large \vec{V}_{I_2/R_0}=(R\dot{\theta}+r\dot{\phi})\vec{e_{\theta}} \\ \\ \vec{a}_{I_2/R_0}=\frac{d}{dt}([R\dot{\theta}+r\dot{\phi}]\vec{e_{\theta}}) \\ \\ \vec{a}_{I_2/R_0}=[R\ddot{\theta}+r\ddot{\phi}]\vec{e_{\theta}}-\dot{\theta}[R\dot{\theta}+r\dot{\phi}]\vec{e_{r}} \\ \\ \vec{a}_{I_2/R_0}=\frac{d^2}{dt^2}(R\theta+r\phi})\vec{e_{\theta}}-\dot{\theta}\frac{d}{dt}(R\theta+r\phi})\vec{e_{r}} \\ \\ C.I.+RSG\Longleftrightarrow \vec{a}_{I_2/R_0}=\vec{0}

Donc pour respecter le RSG il faudrait que S2 ne bouge pas ?
Pouvez vous me dire si le raisonnement est juste ?

Merci d'avance, bon weekend à tous !

Cinématique du solide indéformable

Posté par
krinn Correcteurre : Cinématique du solide indéformable 19-10-13 à 10:55

bonjour,

tu y es presque:

2) on te demande la condition de non glissement donc on résoud: Vg = 0
mais ça ne change rien au résultat

Citation :
On note I2(S2) et I0(S0); tels que I0 et I2 coïncident en un point I (point coïncidant).

il vaut mieux dire: ... tels que I0 et I2 coïncident avec le point (de contact) I
(ce n'est pas n'importe quel point )

RO' + r' = 0 (1)


3) La relation (1) doit être vérifiée ...

4) c'est dommage, tu as bien calculé a2 sans commettre l'erreur de dire:

Vg = V(I2) = 0 donc a(I2) = 0

mais tu te plantes dans ta conclusion:

a2 n'est pas nul (s'il y a mouvement)

a2 = (RO"+r") eo -(rO'2+rO'') er

la vitesse de I2 (S2) n'est nul qu'au moment du contact, mais cette vitesse varie au cours du temps
donc dV(I2)/dt = a2 0


sauf erreur matinale

Posté par
TheBartovre : Cinématique du solide indéformable 19-10-13 à 11:22

Effectivement, il était tard... j'ai pas saisi que la condition de "non-glissement" revenait à dire que l'on a un "RSG" ^^ Désolé ! J'avais mal lu en lisant "trouver la condition de non RGS". Bref ! Mea maxima culpa..

donc, de 1) à 3) tout est correct niveau calcul ?

Pour la 4), je ne comprends pas, vous dites que \vec{a}_{I_2} = \vec{0} SEULEMENT au moment du contact ; mais comme I0(S0) est fixé arbitrairement, on devrait avoir cette relation I0, donc t.

Autre question, la relation (1)dt (ie R\theta+r\varphi=0) correspond à quoi physiquement ? Je n'arrive pas à me représenter cela.

Posté par
krinn Correcteurre : Cinématique du solide indéformable 19-10-13 à 12:39

Citation :
1) à 3) tout est correct niveau calcul ?

à mon avis, oui (sinon qqun te le dira; c'est l'avantage d'un forum

4) j'ai dit: la VITESSE de I2 est nulle uniquement lors du contact, mais son accélération n'est pas nulle
ce qu'il faut bien voir, c'est que I, I2 et Io changent à tout instant, les calculs de vitesse et d'accélération faits ici pour I2 ne valent qu'au moment du contact (avec des points I,Io,I2 dépendant du temps ), mais cela permet néanmoins de trouver une relation générale liant O et dasn le cas du non glissement.

Citation :
Autre question, la relation (RO'+r' ) correspond à quoi physiquement ?


c'est une relation entre paramètres de position qui ne sont pas indépendants s'il n'y a pas glissement, c'est tout

RO' = -r'
donc RO = -r + K en intégrant

avec les C.I.: RO = -r

ce qui me fait penser que l'expression de a(I2) se simplifie et ne s'exprime qu'en fonction d'un des paramètres (O ou )


sauf erreur

Posté par
TheBartovre : Cinématique du solide indéformable 19-10-13 à 13:05

D'accord, merci bien Krinn. Tes explications sont très claires !

PS : En effet, \vec{a}_{I_2/R_o} se simplifie car j'ai pu l'exprimer en fonction de R\theta+r\phi(0 pour RSG). (cf. mes 2 dernières lignes en Latex de mon 1er message)


Bon weekend !

Posté par
krinn Correcteurre : Cinématique du solide indéformable 19-10-13 à 13:33

que trouves - tu pour a(I2) /Ro ?

Posté par
TheBartovre : Cinématique du solide indéformable 19-10-13 à 13:52

Je note \gamma=R\theta+r\phi

\Large \vec{a}_{I_2/R_o}=\frac{d^2\gamma}{dt^2}\vec{e}_{\theta}-\dot{\theta}\frac{d\gamma}{dt}\vec{e}_{r}

démonstration dans mon premier message.
Sauf erreur bête...

Posté par
krinn Correcteurre : Cinématique du solide indéformable 19-10-13 à 14:09

oui mais (t)=0 donc ça fait: a(I2) = 0, tu vois tout de suite le souci

Posté par
TheBartovre : Cinématique du solide indéformable 19-10-13 à 14:14

Ben oui, justement. C'est pour ça que je ne comprends pas ! :/ Ma démonstration me parait juste pourtant.. (celle-ci : )

Posté par
TheBartovre : Cinématique du solide indéformable 19-10-13 à 14:17

Et vous êtes bien d'accord pour la vitesse de I : ? (en mettant des = à la place des )


Si oui, je ne vois pas mon erreur...

Posté par
krinn Correcteurre : Cinématique du solide indéformable 19-10-13 à 17:28

la vitesse de glissement est bonne.
c'est le calcul de l'accélération qu'il faut revoir.

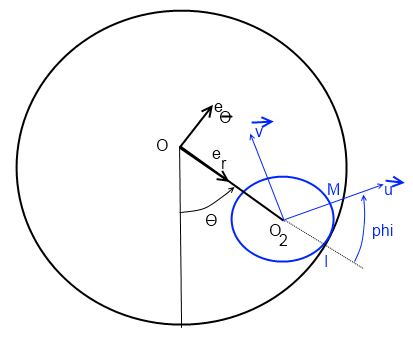
considérons le point M appartenant à S2 (cf dessin)

exprimons V(M)/Ro

OM = OO2 + O2M = (R-r)\vec{e} r + r
donc
V(M) = (R-r)O'\vec{e} o + r d/dt |Ro
= (R-r)O'\vec{e} o + r(O'+')

donc si M I2
V(M) (Ro'+r') \vec{e} o


et \vec{a} (M) = d V(M) / dt

si tu exprimes \vec{a} (I2) tu vas voir qu'il y a bien une accélération normale (selon er donc)


sauf erreur

Cinématique du solide indéformable

Posté par
TheBartovre : Cinématique du solide indéformable 19-10-13 à 18:02

Ah, d'accord ! Il faut se placer dans le cas général pour ne pas perdre d'informations lors de la dérivation.

Merci encore pour toutes ces aides


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !