Niveau licence

Cinématique du solide

Posté par
Nerf 21-10-21 à 19:07

Bonsoir. Svp aidez moi à faire un schéma sur cet exercice.

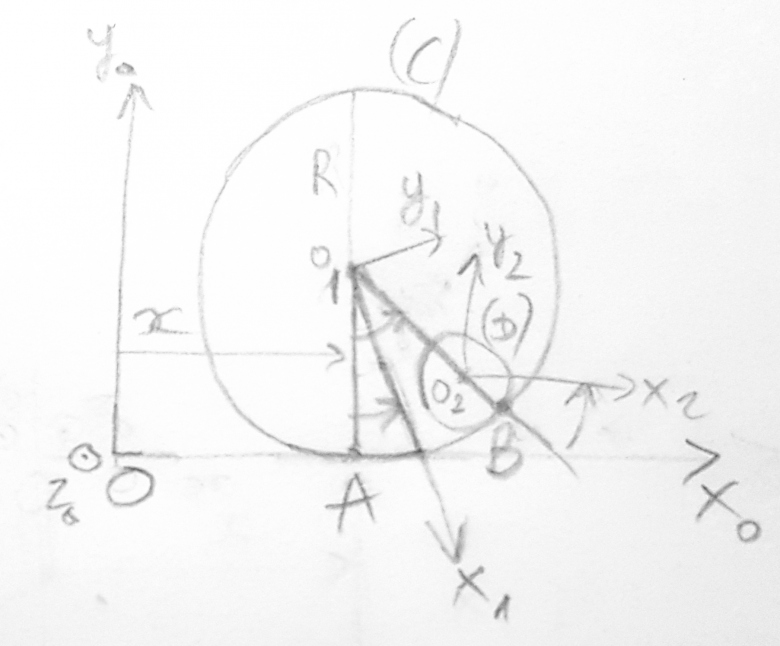
On considère un plan vertical muni du repère Ro(O;xo;yo) avec xo horizontal et yo vertical ascendant. Un cerceau (C) de centre O1 de rayon R et d'un disque (D) de centre O2 de rayon r<R, contenus dans ce plan,se meuvent en étant astreints aux liaisons suivantes: (C) reste au contact de (O;xo) et (D) reste tangent intérieurement à (C). Soient A le point de contact de (C) avec (O;xo), B celui de (C) avec (D), (O1;x1) un axe lié à (C) et (O2;x2) un axe lié à (D). La position du système dans Ro est repérée par l'abscisse x de O1, $\varphi= (\vec{{O_1}A};\vec{x_1}); \theta =(\vec{{O_1}A};\vec{{O_1}B}) et \alpha=(\vec{{O_1}B}; \vec {x_2}), mesurés autour de \vec{z_o}$ (zo=xo^yo).
On note R101;x1 ; y1) et R2O2;x2;y2) les repères liés respectivement à (C) et (D), $\vec{{O_1}B}=R\vec n, \vec v= \vec{z_o}\wedge\vec{{y_o}}$

Posté par re : Cinématique du solide 21-10-21 à 20:34

Bonsoir,
Curieux qu'il n'y ait pas de croquis car cest loin d'etre simple.
Voici un debut de schema possible, si j'ai bien lu,
à refaire au propre et à compléter.

Cinématique du solide