Inscription / Connexion Nouveau Sujet
Cinématique du point (Fête Foraine).
Bonjour,
J'ai un exercice sur la cinématique du point mais j'ai un léger mal à répondre à une question. Pouvez-vous me dire si mon raisonnement est juste ? Voici l'énoncé :
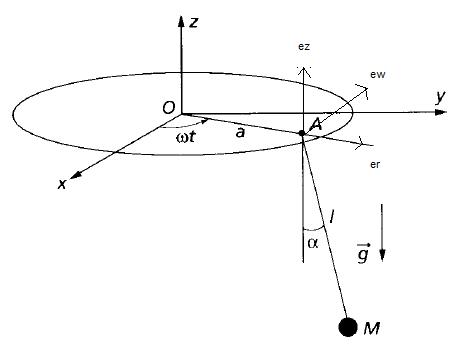
Un manège est constitué de nacelles suspendues par des câbles. On modélise une nacelle par un point matériel M de masse m, et le dispositif de suspension par un fil inextensible de longueur l. On note A le point d'attache supérieure du fil. On admettra que le fil exerce sur la nacelle une force T colinéaire à MA, la tension du fil. On constate que lorsque le manège tourne assez longtemps à vitesse angulaire constante ,w le fil de suspension de la nacelle fait un angle a constant par rapport à la verticale, dans le plan vertical contenant l'axe Oz et
le point d'accrochage A.
1. On note (er, eq, ez) la base locale en A des coordonnées cylindropolaires. Le point A décrivant un mouvement circulaire de rayon a à la vitesse angulaire w, exprimer son accélération par rapport au référentiel terrestre.
2. Décrire le mouvement de M et donner l'expression de son accélération par rapport au référentiel terrestre.
3. Déterminer la vitesse angulaire pour laquelle on obtient 
=
/4 , le référentiel terrestre étant supposé galiléen. Application numérique : a = 3,0 m ; l = 2,0 m.
J'en suis à la question 2.
Dans le doute, je donne l'accélération trouvé pour la question 1 : accélération=-aw²er.
Je poste ce que j'ai trouvé pour la question 2 dans le prochain message.
Merci d'avance,
sabotage.
M a un mouvement circulaire uniforme (faut-il le prouver ou cela suffit ?).
J'ai projetté M orthogonalement sur (OA) car M est dans le plan (ez , er). M' est le projeté orthogonal.
L'angle (MA , MM') =
Donc AM' = sin .
Dois-je travailler avec le vecteur position OM' ?
M décrit un cercle à la vitesse angulaire w.
Le rayon de ce cercle est a + l*sin(alpha) = 3 + 2sin(alpha)
Dans un référentiel lié à la nacelle:
Force centrifuge sur la nacelle = mw²(3 + 2sin(alpha))
Le poids P = mg peut se décomposer en 2 forces:
L'une dans la direction de la corde, elle est compensée par la traction dans le câble de même norme, même direction mais de sens opposé.
L'autre horizontale dirigée vers le centre du cercle et de norme: mg*tg(alpha)
On a: mw²(3 + 2sin(alpha)) = mg*tg(alpha)
w²(3 + 2sin(alpha)) = g*tg(alpha)
Pour avoir alpha = Pi/4 -->
w²(3 + 2sin(Pi/4)) = g*tg(Pi/4)
w²(3 + V2) = 10
w = 1,5 rad/s
-----
Sauf distraction, vérifie. 
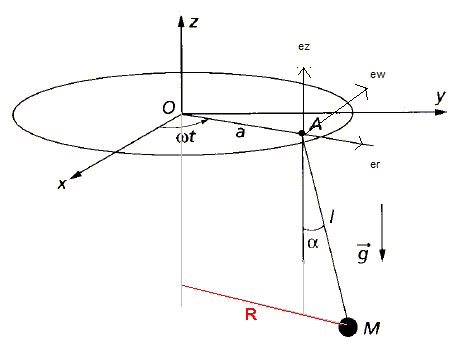
Force centrifuge = mw²R
avec R le rayon du cercle parcouru par la nacelle.
Et ici R = a + l.sin(alpha)
Sauf distraction.
Annuler
connectez vous