Inscription / Connexion Nouveau Sujet
Cinématique du point encoordonnées cartésiennes
Bonjour, je vous remercie par avance de votre aide car je ne comprend vraiment pas cet exercice et j'aimerai un peu d'aide.
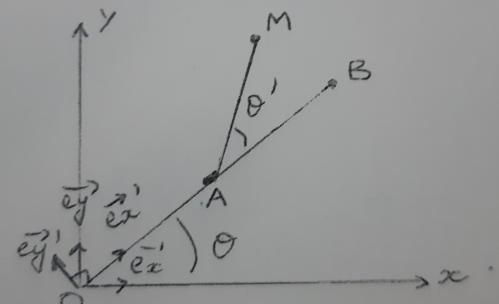
Une barre OB, de longueur 2a, et de milieu A, tourne autour d'un axe Oz à la vitesse angulaire ω constante. Une deuxième barre AM de longueur a tourne autour de l'axe (A, vecteur ez), à la vitesse angulaire ω' constante par rapport à la barre OB.
On définit le référentiel R lié à (Ox, Oy, Oz) et le référentiel R' lié à la tige OB.
On définit les bases de vecteurs orthonormées directes suivantes : (vecteurs ex, ey, ez) et (vecteurs e'x, e'y, e'z).
On suppose qu'à t=0, AM est confondue avec AB, elle-même confondue avec l'axe (Ox).
1. Déterminer l'expression de la vitesse vecteur vM/R' du point M dans le référentiel R'. On exprimera ce vecteur dans la base (vecteurs e'x, e'y, e'z) en fonction de a, ω'.
2. Déterminer l'expression de la vitesse vecteur vM/R du point M dans le référentiel R. On exprimera cette vitesse dans la base de vecteurs (e'x, e'y, e'z) en fonction de a, ω' et ω.
3. Calculer l'accélération du point M dans R en fonction de ω, ω', vecteur AM et vecteur OA.
Bonsoir
Commence par faire un schéma propre que tu pourras scanner et poster ici. Poste aussi ce que tu as réussi à faire et ce que tu ne comprends pas.
Tout d'abord, merci de votre réponse.
Alors pour la question 1, je me suis placée dans la base (vecteurs e'x, e'y, e'z).
Comme le point M a une trajectoire circulaire de centre A, alors le vecteur vitesse, tangent à la trajectoire, sera perpendiculaire à AM. Mais ensuite, comment relier ces informations à la vitesse angulaire ω' et à mes vecteurs e'x et e'y?
Dans le repère R', la vitesse de M peut effectivement se mettre sous la forme :
où est un vecteur unitaire que tu peux facilement exprimer en fonction de
et de
.
Ensuite, il te faudra trouver la vitesse d'entraînement de M pour obtenir la vitesse absolue, c'est à dire la vitesse dans R.
Merci, mais je ne vois pas comment vous représentez le vecteur e ' par rapport aux vecteurs e'x et e'y et qu'est-ce que vous appelez la vitesse d'entrainement de M?
' par rapport aux vecteurs e'x et e'y et qu'est-ce que vous appelez la vitesse d'entrainement de M?
Désolée si mes questions vous paraissent idiotes.
C'est un vecteur colinéaire au vecteur vitesse donc, comme tu l'as écrit, un vecteur perpendiculaire à AM donc un vecteur tel que l'angle :
Il faut le représenter sur la figure puis faire les projections habituelles.
Mais du coup dans l'expression du vecteur vM/R', ce n'est pas seulement en fonction de a et ω', il y a aussi du cos θ et du sin θ non?
qu'est-ce que vous appelez la vitesse d'enfantinement de M?
Dans la mesure où l'énoncé demande de déterminer la vitesse dans R' avant de déterminer la vitesse dans M, on peut penser que le concepteur de cet énoncé s'attend à ce que les étudiants utilisent la méthode dite de "composition des vitesses et des accélérations", méthode utilisant les notions de vitesse relative et de vitesse d'entraînement. Si tu n'as pas étudié cette méthode, le calcul direct de la vitesse dans R est possible mais un peu fastidieux...
Ah... justement on n'a toujours rien vu de nouveau par rapport au programme de terminale donc je ne vois pas comment faire.
As-tu réussi à obtenir la vitesse dans R' ?
Sans cours de niveau (bac+1), cet exercice me parait difficile... Cet exercice est demandé par ton professeur ou tu l'as trouvé dans un livre ? Dans la seconde hypothèse, je te conseille d'attendre un peu et d'avoir vu le cours de cinématique de niveau (bac+1) pour le traiter.
Si cet exercice est demandé par ton professeur, je te propose la méthode suivante qui a l'avantage de ne pas faire intervenir de nouveautés par rapport à la terminale :
Exprimer le vecteur position dans la base mobile
puis dériver par rapport au temps dans le repère fixe R. Attention : ces vecteurs unitaires sont de norme constante mais ils tournent au cours du temps : leurs dérivées par rapport au temps ne sont donc pas nulles.
Mais du coup dans l'expression du vecteur vM/R', ce n'est pas seulement en fonction de a et ω', il y a aussi du cos θ et du sin θ non?
Plus précisément : cos(
 ') et sin(
') et sin( ') interviennent dans le résultat demandé.
') interviennent dans le résultat demandé.Re bonjour.
Alors du coup c'est bien mon professeur qui me demande cet exercice (sinon ça serait pas drôle… ).
Pour la première question, en exprimant le vecteur eθ' avec les vecteurs ex' et ey' (la vitesse est nulle selon ez'), j'obtiens vecteur VM/R'=aω'(-sin(θ')(vecteur ex')+cos(θ')(vecteur ey')).
Déjà, est-ce que c'est bon ? Mais dans le sujet on me demande seulement en fonction de a et ω' et je ne vois pas comment faire.
Merci beaucoup de votre aide
Bravo ! C'est bien cela !
Pour la suite et à titre provisoire, je te conseille d'oublier ce que j'ai écrit sur la composition des vitesses et des accélérations et d'utiliser la méthode décrite hier dans mon message de 23h35. Tu vas obtenir un résultat dépendant des variables a,  et
et  ' mais aussi des sinus et cosinus des angles
' mais aussi des sinus et cosinus des angles  et
et '.
'.
Alors, à la fin de la question 1, après avoir obtenu la vitesse en fonction de ω' et θ', on sait que ω'=dθ'/dt donc θ'(t)=ω't.
Donc finalement, (en mettant les vecteurs en gras) vM/R'=aω'(-sin(ω't)ex'+cos(ω't)ey').
Ensuite, pour la question 2, comme vous me l'avez dit, j'ai exprimé OM dans la base mobile (ex',ey'), cela me donne OM=OA+AM=(a+acosθ')ex'+asinθ'ey'.
Ensuite je dérive par rapport au temps donc vM/R=-aω'cos(ω't)ex'+(a+acos(ω't))(dex'/dt)+aω'cos(ω't)ey'+(asin(ω't))(dey'/dt)
Et là je ne sais pas du tout comment dériver mes vecteurs unitaires.
Si vous pouviez m'aider, merci d'avance


