Inscription / Connexion Nouveau Sujet
cinématique du point - cardioïde
Bonjour voici l'exercice qui me pose problème :
"Un mobile noté M supposé ponctuel décrit la courbe plane dont l'équation en coordonnées polaires (r,
) est :
r = (a/2) (1+ cos )
où a est une constante positive.
L'angle varie avec le temps selon la loi horaire :
(t) = 
t
où la vitesse angulaire du point M est constante.
1) Dans un repère cartésien,
a) déterminer les coordonnées (x,y) du point M et donner la norme du vecteur
position OM
b) exprimer 
en fonction du temps en s'aidant des formules
trigonométriques :
sin (2a) = 2 sin a cos a
cos (2a) = cos2 a - sin2 a
c) exprimer la norme de la vitesse sous la forme
= a
' cos (/2)
en s'aidant des formules :
cos a cos b = 1/2 (cos (a+b) + cos (a-b))
sin a sin b = 1/2 (cos (a-b) - cos (a+b))
1 + cos a = 2 cos2 (a/2)"
Je n'arrive pas à démarrer l'exercice. L'équation donnée est en coordonnées polaires mais on me demande des cartésiennes... Et la forme n'est pas un cercle parfait...
Merci d'avance pour votre aide et vos réponses.
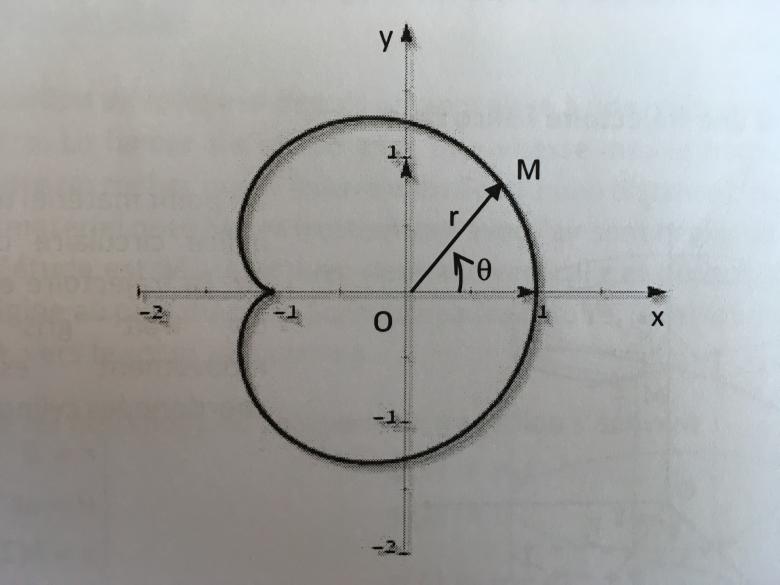
Tout d'abord, il me semble que la figure représentant une cardioïde est erronée.
Pour l'équation polaire donnée, le point de rebroussement devrait se situer à l'origine de l'axe des abscisses, le rayon vecteur étant issu de ce même point. De plus, la courbe devrait traverser cet axe au point d'abscisse a .
Je n'en sais rien désolée j'ai juste pris en photo la figure dans l'énoncé de l'exercice ce n'est pas moi qui l'ai faite
Bonjour Priam, Bonjour Basketteuse06
Juste un schéma pour illustrer le message de Priam de 15h12. J'ai choisi le cas particulier a=1. J'ai noté l'angle polaire comme sur le schéma alors que l'énoncé utilise la lettre ...
Je laisse Priam continuer à gérer ce post... 
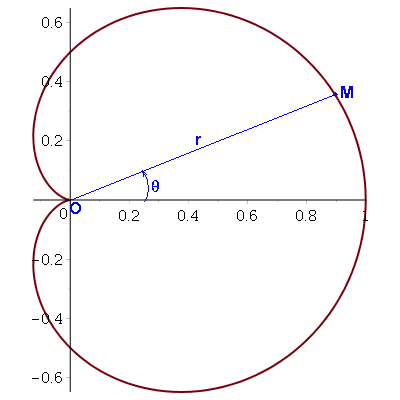
La figure correcte est celle-ci :
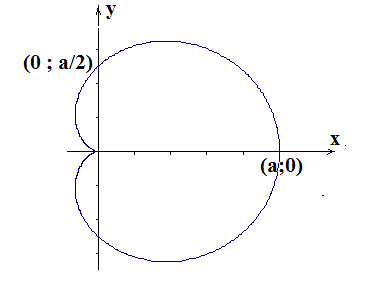
x = r.cos(theta)
y = r.sin(theta)
M(x;y)
|OM| = RCarrée(x² + y²) = |r|
|OM| = (a/2).(1 + cos(theta))
-----
b)
x = r.cos(theta)
y = r.sin(theta)
x = (a/2)*(1+cos(theta)).cos(theta)
y = (a/2)*(1+cos(theta)).sin(theta)
x = (a/2)*(1+cos(wt)).cos(wt)
y = (a/2)*(1+cos(wt)).sin(wt)
dx/dt = (a/2) * [-w.sin(wt).cos(wt) - w.sin(wt).(1 + cos(wt))]
dy/dt = (a/2).[-w.sin(wt).sin(wt) + w.cos(wt).(1 + cos(wt))]
dx/dt = (a/2) * [-w.sin(wt).cos(wt) - w.sin(wt) - w.sin(wt).cos(wt)]
dy/dt = (a/2).[-w.sin²(wt) + w.cos(wt) + w.cos²(wt)]
dx/dt = -(a/2) * w.(sin(2wt) + sin(wt))
dy/dt = (a/2) * w.(cos(wt) + cos(2.wt))
|v|² = [-(a/2) * w.(sin(2wt) + sin(wt))]² + [(a/2) * w.(cos(wt) + cos(2.wt))]²
|V|² = (a²/4).w².[(sin(2wt) + sin(wt))² +(cos(wt) + cos(2.wt))²]
|V|² = (a²/4).w².[2 + 2.sin(wt).sin(2wt) + 2.cos(wt).cos(2wt)]
|V|² = (a²/2).w².[1 + sin(wt).sin(2wt) + cos(wt).cos(2wt)]
|V|² = (a²/2).w².[1 + cos(2wt-wt)]
|V|² = (a²/2).w².[1 + cos(wt)]
|V|² = (a²/2).w².2.cos²(wt/2)
|V|² = a².w².cos²(wt/2)
|v| = |a.w.cos(wt/2)|
Et avec theta(t) = w.t -->
|v| = |a.w.cos(theta/2)|
A comprendre et à vérifier bien entendu.
Annuler
connectez vous