Inscription / Connexion Nouveau Sujet
Cinématique du point
Bonjour, j'espère que vous allez très bien. J'ai besoin d'aide pour comprendre le début de correction d'un petit exercice.
Voici l'énoncé de l'exercice:
Dans cet épisode de la Guerre des étoiles, on peut assister à une course poursuite de « speeder » entre des cheminées d'usine. On suppose que le véhicule suit une trajectoire sinusoïdale de slalom entre les cheminées alignées selon l'axe (Ox). Elles sont espacées d'une distance L = 200 m.
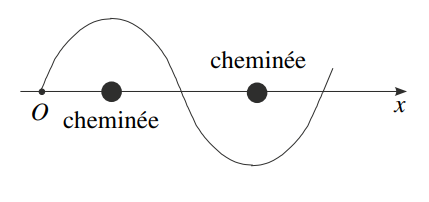
1. Le véhicule conserve une vitesse v0 constante selon (Ox) et met tt = 12 s pour revenir sur l'axe après la sixième cheminée. En déduire la vitesse v0. Faire l'application numérique.
2. Déterminer l'amplitude de la sinusoïde pour que l'accélération reste inférieure à 10g en valeur absolue, avec g = 9,8 m·s−2. Que penser des valeurs obtenues ?
Début de la solution:
On choisit un repère cartésien (O,x,y) et on note vect(ux) et vect(uy) les vecteurs de base. L'équation de la trajectoire, telle qu'elle apparaît sur la figure, s'écrit y = asin(2πx/L)
Mon problème c'est qu'en voyant cette équation on dirait que la période de la sinusoïde est L alors que c'est 2L selon moi. Donc on devrait plutôt avoir y=a sin( x/L).
x/L).
En résolvant le problème, je trouve que l'amplitude de la sinusoïde doit être <= 39,7 m
A arrondir à 2 chiffres significatifs si on suit les règles habituelles.
Si ta correction n'arrive pas à cela ... il y a un soucis.

Il arrive à a=9,9m.
C'est faux.
Le mieux est que tu essaies de résoudre le problème toi-même ...
et que tu mettes ton raisonnement sur le site.
On pourra alors t'aider à corriger les erreurs.
Rebonjour,
En complément de ma réponse précédente...
Comme il y a une erreur d'un facteur 2 sur la période de la sinusoïde de trajectoire (comme indiqué dans ton message d'origine) ... ce n'est pas étonnant qu'en fin de calcul, il y ait un facteur 2² = 4 sur le calcul de l'accélération, et donc aussi ce même facteur 2² = 4 sur la valeur de l'amplitude de la sinusoïde ...
Et donc, la réponse du corrigé (soit 9,9 m), une fois l'erreur corrigée sur la période de la sinusoïde, deviendrait 9,9 * 4 = 39,6 ... qui est ce que j'ai trouvé aux arrondis de calculs près.
Je vois je vois.
Mis a part cela, je n'ai pas rencontré de difficulté je pense.
Voici mon raisonnement :
On a y=asin(πx/L)
1- Comme il revient sur l'axe Ox après la 6ieme cheminée, il a parcouru une distance de 6L et donc v0=6L/tt
2-La vitesse suivant 0x étant constante, son accélération suivant cette axe est nulle et x(t)=v0t en prenant x(0)=0 comme position initiale.
y=a sin(πv0t/L)
En dérivant on a alors ay(t)=-a(πv0/L)² sin(πv0/L)
Comme on veut que l'accélération soit inférieure à 10g en valeur absolue alors on pose : a(πv0/L)²<10g et on tire a


