Inscription / Connexion Nouveau Sujet
Cinematique d'un point ( MPSI )
Bonjour,
je suis tombé sur un exercice, je ne sais ni sa relation avec le cours, ni par quoi commencer, voici l'énoncé :
Trois chats se trouvent initialement aux sommets d'un triangle équilatéral. le premier court après le second qui poursuit le troisième, lui même courant après le premier. Ils courent à la même vitesse et celle-ci reste constante pendant toute la poursuite.
1) Déterminer la durée de la poursuite.
2) En déduire la distance parcourue par chacun des chats.
3) Déterminer l'équation de la trajectoire de l'un des chats en coordonnées polaires.
merci d'avance.
Bonjour
Tu ne précises pas la manière dont se déplacent les chats. Si, comme je le pense, chaque chat adapte constamment la direction de son vecteur vitesse pour se diriger vers le chat qu'il poursuit, tu as ici un problème de poursuite pas particulièrement simple, sûrement pas le type de problème abordé en début de MPSI !
Tu as quelques indications ici : 
.
Quelques indications sur un problème de poursuite plus simple :
tu as ici un problème de poursuite pas particulièrement simple
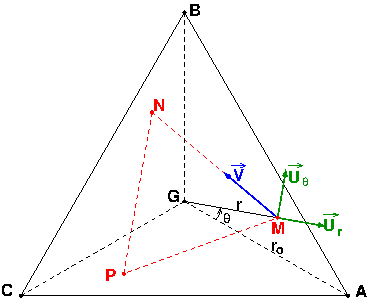
Quoique... En réfléchissant bien... Le plus difficile consiste à bien comprendre pourquoi les trois chats, initialement en A, B et C, à un instant quelconque au cours de la poursuite, occupent toujours les trois sommets d'un triangle équilatéral (MNP) de centre de gravité G (voir schéma ci-dessous). Dans ces conditions, il suffit d'écrire l'expression du vecteur vitesse en coordonnées polaires :
Il faut alors mettre en équation les deux renseignements suivants :
- La norme du vecteur vitesse Vo est une constante ;
- Le vecteur vitesse d'un chat étant constamment orienté vers le chat qu'il poursuit, l'angle entre le vecteur vitesse et le vecteur MG est une constante égale à 30°.
On montre alors simplement que r est une fonction affine de t. Cela permet de déterminer simplement la durée de la poursuite. On obtient ensuite par intégration l'expression en fonction de t de l'angle polaire
. Il est facile alors de montrer que la trajectoire de chaque chat est une "branche" de spirale logarithmique.
Annuler
connectez vous