Inscription / Connexion Nouveau Sujet
Cinématique à 3 phases (2*MRUA + MRU)
Bonjour pouvez m'aider s'il vous plaît ?
exo : Un métro part de la station A et fait un arrêt a la station B,
le métro accélère et décélère de 1 mètres par seconde^2. Déterminer le temps minimal pour parcourir le trajet entre A et B. Distance AB = 4km
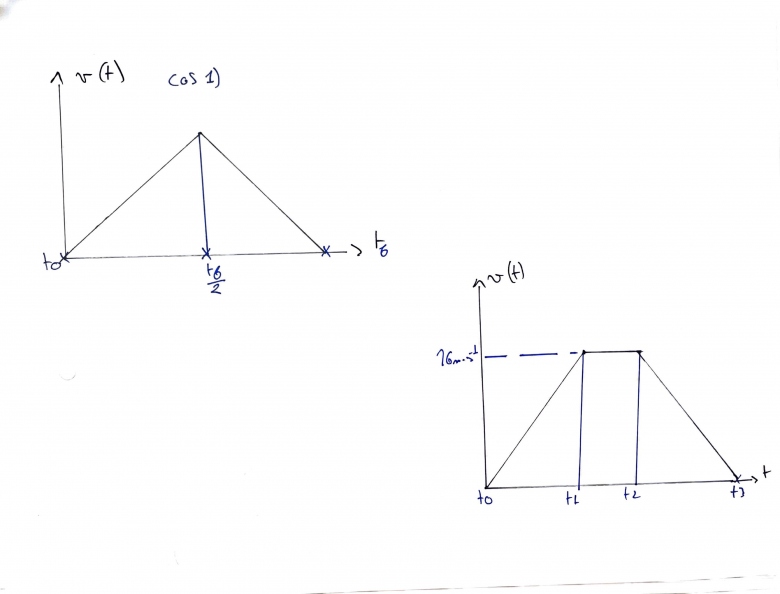
Cas 1 : le métro n'a pas de limite de vitesse
Cas 2 : le métro a une limite de 60km.h
Voila ce que j'ai fait pour le cas 1.
Phase accélération :
a (t) = a = 1
v(t) = at
x(t) = 0,5at^2
Phase décélération :
a (t) = -a = -1 m/s^2
v(t) = -at
x(t) = -0,5at^2
Donc la moitié du temps il accélère et l'autre moitié il décélère.
Temps final = Tf
x(Tf*0,5)=2*10^3 mètres => en utilise : x(t) = 0,5at^2 alors Tf = (8*2*10^3)^0,5 = 126 s
Cas 2:
On vérifie si v(Tf*0,5) > 60*1/3,6 km.h. et donc 126m/s > 16 m/s
Phase 1)
a(t) = a = 1 m/s^2
v(t) = at + v(t0) = t
x(t) = 0,5*a*t^2 = 0,5t^2
Phase 2)
a(t) = 0
v(t) = v = 16 m/s
x(t) = v(t1)*t + CTE
Cherchons t1:
or la vitesse de la phase 1 en t1 est égale à la vitesse de la phase 2 en t1
16 = at1 => t1 = 16 s
Cherchons CTE pour la phase 2 :
or la position en t1 de phase 1 est égale a la position de la phase 2 en t1
a*t1^2 = 16*t1 + CTE => CTE = 0,5*16^2-16^2 = -128 m
Donc pour la phase 2 on a x(t) = v(t1)*t + CTE = 16t -128.
Voila après je me suis dit que je pouvez fair la même chose pour la phase 3 avec le point de jonction qui est t3 mais je bloque car je sais pas comment trouver t3. Ou alors peut être avez vous une autre méthode
Merci de votre aide !
Bonjour
Ta rédaction laisse un peu à désirer en terme de rigueur. En revanche, tu as compris l'essentiel. Je pense qu'il faut partir dans les deux cas des courbes v=f(t) que tu as tracées et rédiger quelque chose de propre.
Pas nécessairement. Dans le premier cas par exemple : que valent les coefficients directeurs des deux segments de droites correspondant à v(t) ?
Cela permet de démontrer simplement que la vitesse maximale est obtenue à la moitié du trajet.
1 pour la phase une et -1 pour la phase deux
Ou 1 et 1 en valeur absolue cela suffit donc il ont le même ont le même coefficient directeur cela suffit pour prouver que la vitesse max est en t/2 ?
Oui je comprends, mais du coup comment faire pour retrouver t3 (temps total) dans le cas 2 s'il vous plaît ?
Tu peux raisonner à partir de la courbe v=f(t).
Puisque le coefficient directeur entre to et t1 vaut a=1m/s2, et que le coefficient directeur entre t2 et t3 vaut (-a), tu peux donc facilement calculer les durées de ces deux phases (t1-t0)=(t3-t2).
Tu as parlé précédemment d'intégration : effectivement la distance parcourue représente l'aire sous la courbe représentative de v(t). Les aires des triangles te donnent donc simplement les distances parcourue pendant ces phase d'accélération et de décélération (tu peux aussi utiliser les équations horaires).
Par différence avec la distance totale AB=4km, tu obtiens la distance parcourue entre t2 et t1 puis la durée (t2-t1)...



