Bonjour
Il s'agit d'un cylindre contenant un petit moteur électrique et une soufflerie qui injecte du gaz par sa base, selon le principe des aéroglisseurs. Le mobile est ainsi sur "coussin d'air" et il peut se déplacer pratiquement sans frottement. Le poids du mobile est, sur une table horizontale, exactement compensé par l'action du coussin d'air si bien que le principe d'inertie s'applique au mobile. Donc ???
Je te laisse continuer...

Bonsoir,

Alors si la trajectoire du mobile est une ligne droite, ça ne peut pas être un cercle. En fait le centre de gravité du mobile se déplace en ligne droite (vitesse , voir système de coordonnées défini ci-dessous), et le mobile tourne sur lui-même simultanément (rotation selon l'axe défini ci-dessous, vecteur rotation ).



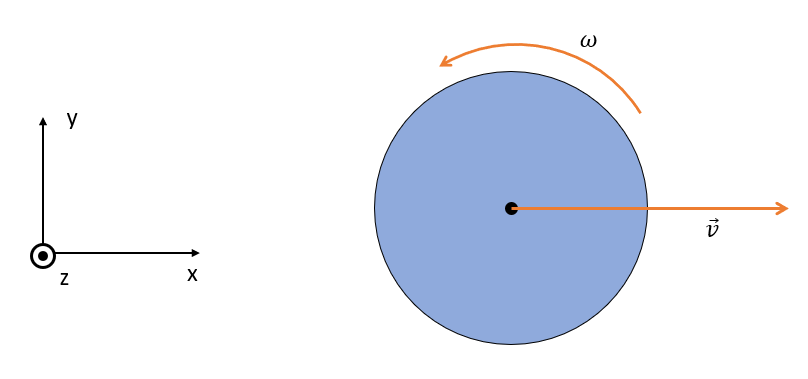
Est-ce que tu comprends mieux la situation ?

Bonjour athrun
En bas de l'éditeur de texte il existe une phrase en rouge " Vérifier la présence de nouvelles réponses " sur laquelle on peut cliquer pour éviter les messages croisés. Mais bon : ton message est intéressant !

Un grand merci à tous les deux !

On me demande quelles forces sont appliquées au mobile à un instant t quelconque : j'ai dit vecteurs P et R qui se compensent

On me demande d'en déduire les vecteurs accélération et vitesse
Comme la somme des vecteurs P et R =0 alors le vecteur a = vecteur nul et Vx=Vo et Vy=0

D'où G , le centre de masse a un mouvement rectiligne uniforme
donc sa trajectoire est une droite

Est-ce correct? merci

Merci .

Donc si je travaille maintenant dans le repère d' origine G et de mêmes axes x et y , le mouvement du mobile est circulaire uniforme ?

Oui dans la mesure où les frottements sont négligeables.

Pardon vanoise, ça fait longtemps que je ne suis pas venu sur le forum et j'avais oublié l'existence de cette fonction pratique ^^

Merci .

Excusez moi d'abuser encore mais on me demande à la fin de l'exercice de choisir un repère dont l'axe (Ox) est parallèle et de même sens que le vecteur vitesse de G et de dessiner l'allure de la trajectoire d'un point M périphérique

1) si on a pas donné initialement de mouvement de rotation au mobile
2) si on a donné une vitesse linéaire de rotation plus rapide ou moins rapide que vG
3)si on a pas donné de vitesse de translation au mobile

Je sèche....

Tu peux très facilement répondre pour les cas 1 et 3. Pour le cas 2 : c'est effectivement plus compliqué ; il faut distinguer trois cas selon que V_G est supérieur, égal ou inférieur au produit R.. R désigne le rayon du mobile auto-porteur. Je ne sais pas si cela est à ton programme : la trajectoire dans le repère du laboratoire du point M dans le cas particulier V_G=R. s'appelle une cycloïde. Commence par réfléchir aux cas 1 et 3...

Merci .

Pour le cas 1) je dirais que le mobile a un mouvement rectiligne uniforme tout le temps comme son centre de masse .

Pour le cas 3) le mobile reste immobile

Est- ce correct ?

Cas 1 : le mobile a un mouvement de translation rectiligne uniforme ; donc le mouvement du point M à la périphérie ?
Cas 3 : Le point G est immobile mais le point M?

Cas 1 : Le point M périphérique a un mouvement rectiligne uniforme aussi

Cas 3 : Le point M périphérique tourne autour du point G

Je me trompe?

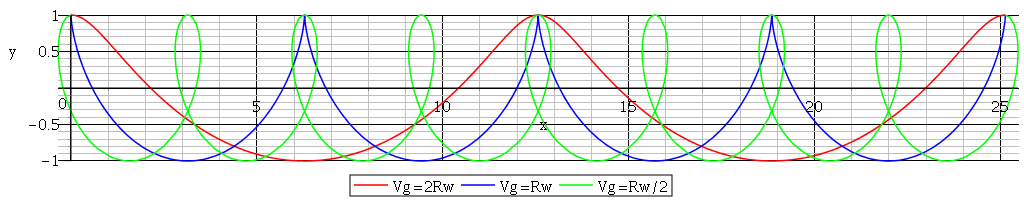
OUI. Dans le cas 3 : on peut parler pour M de mouvement circulaire uniforme. Reste le plus difficile. Tu peux partir du schéma proposé par athrun et étudier les trois cas comme expliqué dans mon message du  15-02-22 à 19:01. Pour t'aider un peu, voici trois trajectoires possibles selon les valeurs de R. par rapport à V_G.
Je suppose que, lorsque x_G=0, x_M=0 et y_M=R.

Merci beaucoup

Je vais travailler ça Vanoise

Re!

Excusez moi encore mais les exercices parlent souvent du référentiel du centre de masse et du référentiel de la table

J'ai écrit : Soit G le centre de masse , soit M un point périphérique , soit O l'origine du repère de la table alors

OM = OG + GM en vecteurs ( relation de Chasles ) nous permet de passer des coordonnées de M qui sont celles du vecteur OM (référentiel table) à celles de M qui sont celles du vecteur GM (référentiel centre de masse)

Est-ce correct?

Merci

L'idée de faire intervenir le référentiel barycentrique R_G est intéressante car, dans ce référentiel, le mouvement du point M est tout simplement un mouvement circulaire uniforme à la vitesse angulaire .
Je pense que tu connais la relation dite de composition des vitesses.Elle donne ici simplement :

Oui merci beaucoup Vanoise !