Inscription / Connexion Nouveau Sujet
Cinématique
Bonjour , j'ai une petite question a propos d'un exercice sur la cinématique svp 
Deux voitures A et B roulent à la suite l'une à la suite de l'autre à la même vitesse de 90km/h en ligne droite . La distance AB est alors égale à 30 m. pour éviter un obstacle, la première voiture A freine avec une acceleration de -4m/s². La voiture B freine avec la même acceleration une seconde plus tard.
On suppose que le mouvement s'effectue selon un axe horizontal (Ox) en prenant comme origine des temps l'instant où la deuxieme voiture freine . A cet instant , la position de ce vehicule coincide avec l'origine de l'axe (Ox).
On souhaite établir les equations horaires du mouvement pour les voitures A et B à un instant t>0 .
Donc je les ai bien trouvées et elles valent :
conditions initiales :
A: a(A0)=-4m/s² v(A0)=21m/s x(A0)=28m
B: a(B0)=-4m/s² v(B0)=25m/s x=(BO)=0m
et donc :
On me demande ensuite si les deux voitures vont à un moment se percuter et si oui à quel instant :
alors si on fait xa=xb je trouve que t=7sec et c'est la bonne réponse
Mais mon problème est :
si j'avais utilisé les equations de la vitesse et isoler t pour lequel leur vitesse a A et B soit nulle , je trouve :
va=0 si t=5.25s
vb=0 si t=6.25
puis je reinjecte ce temps dans les equations horaires et je trouve 78 et 85m, la position pour laquelle les deux voitures vont s'arreter.
Mais du coup avec ceci je vois que les deux voitures ne s'arrete pas au même moment ni a la même position (78 et 85m) donc c'est la que je ne comprends pas trop
Merci d'avance 
Bonjour
Je ne comprends pas bien pourquoi tes deux vitesses initiales sont différentes. 0 quelle situation précise correspond la date t=0 ?
Bonjour, enfaite j'ai pas posé tout l'énoncé à vrai dire :
la question qui precedait la mienne était :
On suppose que le mouvement s'effectue suivant un axe horizontale (Ox) en prenant comme origine des temps l'instant où le vehicule A freine. A cet instant, l'origine 0 de l'axe est confondue avec la position de B .
Et donc on me demande ici, de calculer au moment où le vehicule B freine :
-la distance A et B
- la vitesse de la voiture A
et donc a ce temps t=0 ( donc quand A freine) :
A: aA0=-4m/s² vA0=25m/s xA0=30m
B : aB0=0m/s² vB0=25m/s xB0=0m
et donc au temps t=1s donc quand B freine (comme le dit la consigne) :
va=21m/s
vb=25m/s
et donc ce temps=t=1s correspond au temps t=0s de ma consigne (cf 1er post)
Desolé si c'est un peu l'embrouille et le desordre dans mes posts
Merci pour ta précision. Je comprends maintenant !
si on fait xa=xb je trouve que t=7sec et c'est la bonne réponse
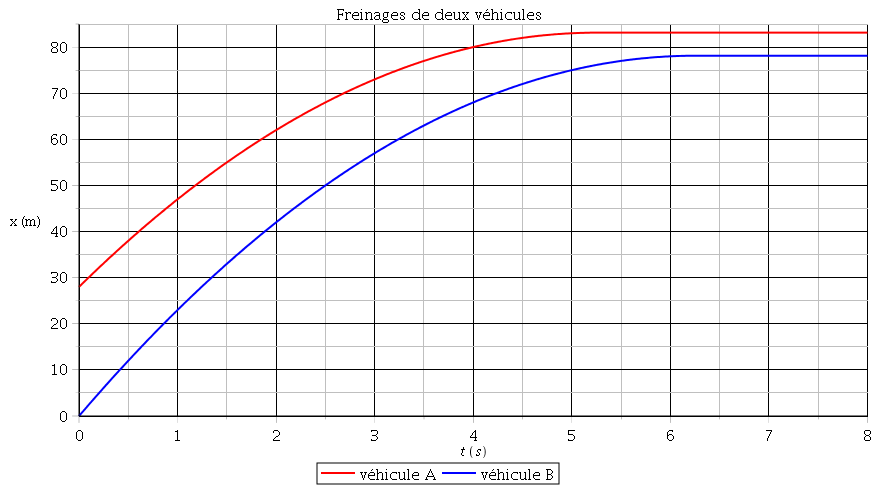
Tu as bien raison d'avoir des doutes car la réponse est fausse ! Les équations horaires que tu as écrites ne sont valides que si les véhicules possèdent une vitesse positive. Lorsque leurs vitesses s'annulent, ils s'immobilisent définitivement, ils ne repartent pas en arrière d'un mouvement uniformément accéléré ! Il faut donc écrire :
J'ai représenté ci-dessous les variations en fonction de t de xa et xb : on voit clairement que la collision n'a pas lieu ; on obtient toujours : xa>xb !
D'accord merci,
par contre pourriez vous reposter votre réponse car vos calculs ne sont pas visibles svp
je comprends mieux pourquoi il n'y a pas de collision
Par contre je ne comprends pas trop le lien entre mes equations horaires et le fait que les voitures ne repartent pas vers l'arriere car mes equations ne sont valables que pour les vitesses positives ?
Merci bcp
Je pense que l'éditeur Tex de formules à un problème comme cela arrive de temps en temps. Je recopie les formules :
xa=-2t2+21t+28 tant que t<5,25s
xa=83,125m si t 5,25s
5,25s
xb=-2t2+25t tant que t<6,25s
xb=78,125s si t 6,25s
6,25s
Supposer tes équations horaires valides quel que soit t positif, suppose que, lorsque chaque véhicule atteint une vitesse nulle, il fait demi tour de façon quasi instantanée et repart en sens inverse d'un mouvement uniformément accéléré.
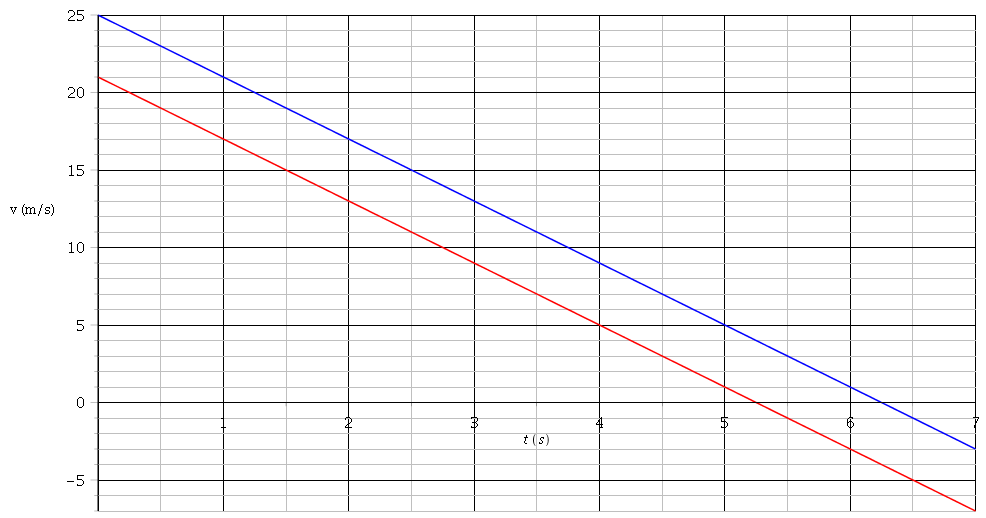
On a toujours : va=-4t+21 mais va<0 pour t>5,25s et vb=-4t+25 mais vb<0 pour t>6,25s.
Les courbes montrent bien l'existence d'un choc en t=7s mais il ne s'agit pas du problème posé. Les véhicules ne font pas demi tour sur route.
Voici les courbes que l'on obtiendrait dans le cas d'un demi tour sur route pour chaque véhicule.