Inscription / Connexion Nouveau Sujet
Cinématique
Bonsoir j'ai besoin de votre aide svp.
Exercice :
Un point M décrit un arc de cercle OA de centre C et de rayon R=2,7m . La trajectoire est orientée de O vers A. Le mobile part de O à t=0 avec une vitesse V0.
A la date t , son abscisse curviligne est S=OM=-0,6t²+3t
1- Donne l'expression de la vitesse V(t) . Calcule V0.
2-En A la vitesse du mobile s'annule .
2-1- Détermine la date en ce point .
2-2 En déduis l'abscisse curviligne de ce point.
3- Détermine, dans la base de Frenet, le vecteur-accélération du point M à la date t=1 s ainsi que sa norme .
4- Détermine l'équation relative à l'abscisse angulaire 
=f(t)
Réponses :
1- Expression de la vitesse V(t) et calcul de V0
V(t)=dS/dt=d(-0,6t²+3t)/dt=-1,2t+3
V(t)=-1,2t+3
A t=0 s , V0=1,2×0+3=3 m/s
2-
2-1 Date en A
En A , V=VA=0
=> -1,2tA+3=0
=> -1,2tA=-3
=> tA=2,5 s
2-2 Abscisse curviligne en A .
SA=-0,6tA²+3tA
=-0,6×(2,5)²+3×2,5
SA=3,75 m
3- Vecteur-accélération dans la base de Frenet et sa norme
A t=1 s
a
=dv/dt=d(-1,2×1+3)/dt=0 m/s²
an=v²/R=(1,8)²/2,7=1,2 m/s²
a=an=1,2 m/s²
4-
=
t+0
S0=R0 => 0=S0/R
=> 0=(-0,6×0²+3×0)/2,7=0 rad
Comment déterminer ?
Bonjour,
3) attention! il faut calculer a = dv/dt = ... et ensuite prendre sa valeur en t =1s, et non pas dériver v(1) qui est forcément une constante!
4) attention! ici le mouvement n'est pas uniforme.
Mais il y a bien une relation entre s(t) et (t)
3) A tout instant t , donc à t=1 s
a=dv/dt=d(-1,2t+3)/dt=-1,2 m/s²
an=1,2 m/s²
a=√(a²+an²)
a=√[(-1/2)²+(1,2)²]=1,7 m/s²
4) De quelle relation parlez vous ?
4) tu as écrit : so=R o
mais en fait la relation a la forme suivante , à toute instant t:
s - so= R( - o ) en tenant compte des conditions initiales : à t=0, s=so=0 et =o = ....
( n'a pas été défini ci-dessus )
Ben je ne sais pas moi , c'est tout ce que L'énoncé dit que j'ai recopié.
Ce que je sais c'est que S=R
À t=0s , S0=R0
Alors on en fait un.
Sur la figure ci- dessous, et s sont definis de facon à ce qu'on puisse ecrire: s=R ce qui donne (t)= ...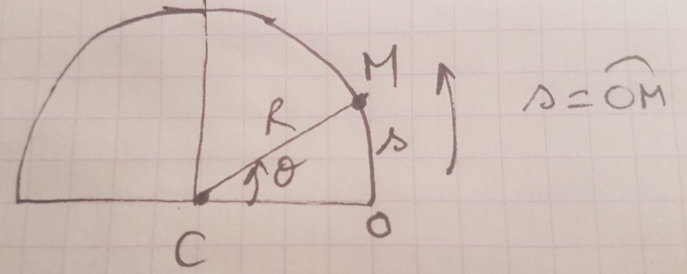
***Image pivotée***
=(-0,6/2,7)t²+(3/2,7)t=-0,2t²+1,1t
Pourquoi le résultat de mon message précédent est différent de celui ci ?
Annuler
connectez vous