Inscription / Connexion Nouveau Sujet
Cinématique
Bonjour,
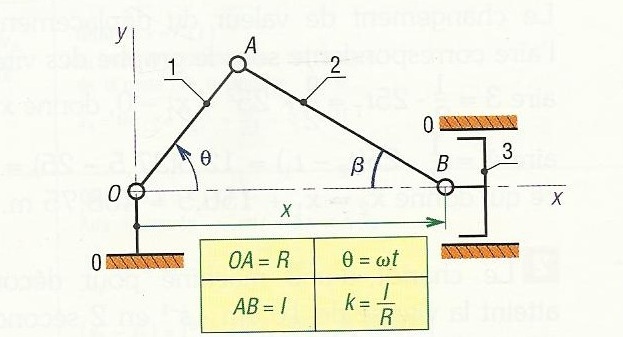
Je fais des exercices basés sur la mécanique histoire de m'exercer et je suis tombé récemment sur un problème à résoudre. Il s'agit d'écrire les équations générales du piston, voir schéma ci-dessous:
Voici mon problème: j'essaye de retrouver les mêmes équations que ceux de la correction mais je suis bloqué à un endroit:
Rsin
=Lsin
x=Rcos+ Lcos, je sais qu'ensuite il faut utiliser la formule cos²+sin²=1
seulement dans la suite de l'exercice on obtient:
x=R(cos+
(k²-sin²))
Et c'est au niveau de(k²-sin²) que je ne comprend pas. Comment l'obtient on?
merci d'avance
x = R.cos(theta) + L.cos(beta) (1)
R.sin(theta) = L.sin(beta)
sin(beta) = (R/L).sin(theta)
sin²(beta) = (R²/L²).sin²(theta)
1 - sin²(theta) = 1 - (R²/L²).sin²(theta)
cos²(theta) = 1 - (R²/L²).sin²(theta)
cos²(theta) = (L² - R².sin²(theta))/L²
cos(theta) = (1/L).V(L²- R².sin²(theta))
L.cos(theta) = V(L²- R².sin²(theta)) (avec V pour racine carrée).
Et dans (1) ---> x = R.cos(theta) + V(L²- R².sin²(theta))
x = R.cos(theta) + R.V[(L²- R².sin²(theta))/R²]
x = R.cos(theta) + R.V[(L/R)²- sin²(theta)]
x = R.cos(theta) + R.V[k²- sin²(theta)]
-----
Sauf distraction. 
bonjour
tu écris que: cos2 = 1 - sin2
et comme cos est ici positif
cos = (1 - sin2 )
puis tu reportes l'autre relation et tu trouves:
cos = (1 - R2/L2 sin2 )
L cos = (L2 - R2 sin2 )
L cos = R (k2 - sin2 )
avec k = L/R
Annuler
connectez vous