Inscription / Connexion Nouveau Sujet
cinématique
bonjour
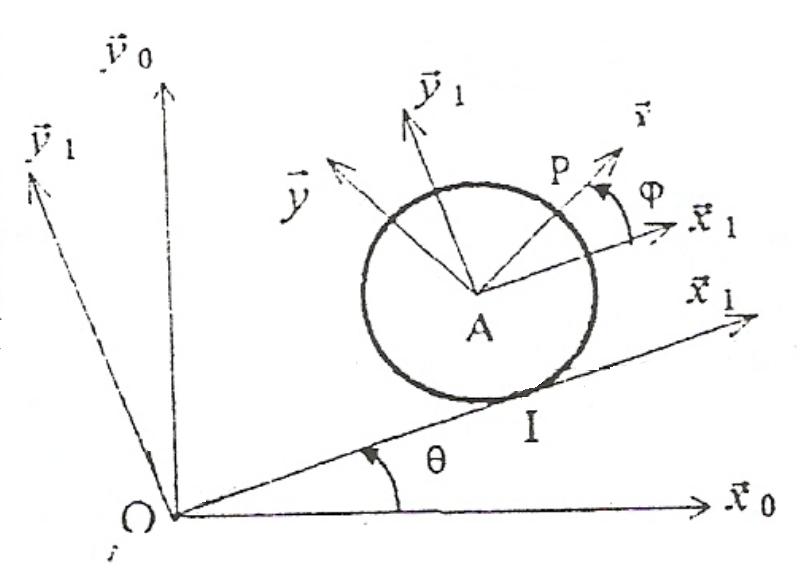
on étudie le mvt de P dans R0(O;x0,y0,z0) considéré comme absolu
si R1(O;x1;y1;z0) est le répère relatif donner les expressions de:
a) des vitesses relative , d'entrainement et absolue au point P.
b) des acélérations relative d'entrainement comlaimentaire et absolue au point P.
je trouve bcp de problèmes dans ce chapitre
la résolution de ce problème me semble délicate
j'éspère trouver votre aide
merci d'avance.
Il s'agit essentiellement d'appliquer des définitions à un mouvement relativement simple.
Où bloques-tu?
C'est effectivement la vitesse de par rapport au repère
qu'il faut calculer mais par contre tes notations ne sont pas très claires, d'autant plus que tu ne les as pas indiquées dans ton premier message.
Je suppose que est le rayon du cercle et
l'abscisse du point
dans le repère
?
Ensuite, pour la vitesse d'entrainement il te faut calculer cette fois la vitesse par rapport à non plus du point
, mais du point lié à
qui coïncide avec P.
Pour la vitesse absolue, il ne te reste qu'à additionner les deux vitesses précédentes.
Dans le repère R1 :
P(K - R.phi - R.(1-cos(phi)) ; R(1 + sin(phi)) avec K une constante.
dx1P/dt = - R.d Phi/dt - R.sin(Phi) d Phi/dt
dy1P/dt = R.cos(Phi) d Phi/dt
Avec R le rayon du cercle
vect(vP) = -R(1 + sin(Phi)) . d Phi/dt. vect(ux1) + R.cos(Phi) d Phi/dt . vect(uy1)
...
-----
Sauf distraction. 


