Quels sont les unités et les labels des axes ? Je crois que tu as inversé les axes

Bonsoir
D'accord avec cercus.
Tu peux aussi te poser les deux questions suivantes (réponses dans le cours de terminale ):
1 : quelle est l'expression théorique de l'accélération lors d'une chute libre  (influence des frottements négligée ) ?
2 : quelle est l'équation horaire x=f(t) pour un mouvement uniformément accéléré avec vitesse initiale nulle ?

Le diagramme montre qu'il y a un soucis ... puisque "prolongé", il ne passe pas par l'origine des axes.

Comme les 4 mesures à Delta x grand ont l'air bien alignées, on "renifle" une erreur constante sur les mesures des temps.

Estimons cette erreur "supposée", soit E cette erreur :

Essayons de calculer E pour que la droite delta x = k.t² (passant par les mesures en 95 cm et 19 cm) passe par l'origine.

0,95 = k.(0,398 + E)²
0,19 = k.(0,158 + E)²

(0,398+E)/(0,158 + E) = RCarrée(0,95/0,19) = 2,236

0,398 + E = 2,236.(0,158 + E)

0,398 + E = 0,3533 + 2,236.E
E = 0,036 s

Il serait fort à parier que le chrono a démarré environ 0,036 s après le lâcher de la bille ... et que donc tous les temps mesurés devraient être augmentés de 0,036 s pour refléter mieux la réalité.

Mais, il n'est pas évident que ce genre de manip soit permises ici.

On peut déjà voir ce que donnerait les calculs en corrigeant tous les temps de + 0,036 s, mais cela me semble pas mal.

Le mieux serait de recommencer une série de mesures, en faisant ce qu'il faut pour éviter l'erreur de départ du chrono ... ou de prévoir "quelque chose" pour mesurer l'erreur de décalage entre le départ de la bille et la mise en marche du chrono, pour corriger les mesures de temps.

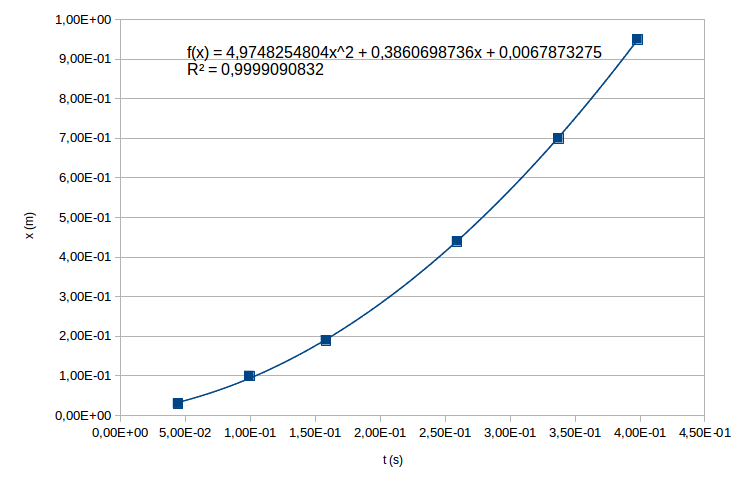
Une façon simple de régler le problème d'un retard de démarrage du chrono consiste à tracé la courbe x = f(t) . Si le mouvement est bien uniformément accéléré , le chronomètre étant déclenché un peu après la mise en mouvement, on va obtenir une équation horaire caractéristique d'un mouvement uniformément accéléré avec vitesse initiale non nulle et avec abscisse initiale non nulle. Dans ce cas, la courbe obtenue est une parabole. C'est bien ce que l'on obtient comme le prouvent la courbe jointe, l'équation de la courbe de tendance et la valeur du carré R² du coefficient de corrélation. On peut donc écrire :
x=A.t²+Vo.t+Xo
La valeur numérique de A permet immédiatement d'obtenir une valeur expérimentale de g. Cela suppose que Chilling revoit son cours de terminale pour répondre aux deux questions suivantes :
1 : quelle est l'expression théorique de l'accélération lors d'une chute libre  (chute avec influence des frottements négligée ) ?
2 : quelle est l'équation horaire x=f(t) pour un mouvement uniformément accéléré avec vitesse initiale  Vo non nulle et abscisse initiale Xo non nulle ?
Remarque 1 : la valeur de g expérimentale est très légèrement supérieure à la valeur admise. Petit problème d'étalonnage du matériel de mesure ?
Remarque 2 : on peut faire une évaluation du retard E au démarrage du chronomètre.
La valeur de E déduite de la valeur de Vo=0,386m/s conduit à E=39,3ms ;
La valeur de E déduite de Xo=6,787mm conduit à E=37,2ms
Ces valeurs sont cohérentes entre elles et diffèrent peu de l'estimation faite par JP à partir de deux points expérimentaux.