Inscription / Connexion Nouveau Sujet
Chute d'une masse, poulie et chariot
Bonsoir à tous!
Lors de l'examen de physique méca, nous avons eu un exercice "simple" que personne à ma connaissance n'a su faire.
Nous avons un système constitué d'un chariot de 10kg, d'une masse de 1kg posé sur le chariot et d'une 2ème masse relié à la première pendue dans le vide. La corde passe dans une poulie qui est accrochée au chariot.
On néglige toutes les forces de frottements dans le système (y compris entre la masse de 1 kg et le chariot).
Au temps t=0, la masse pendue dans le vide est lâchée.
Dans quelle direction va aller le chariot pour un t légerement > 0
Je ne savais pas pour qu'elle raison le chariot avançait, j'ai été demandé à mon professeur aujourd'hui et il m'a dit que la raison était une conservation de la quantité de mouvement. Quelqu'un sait-il m'expliquer?
Merci beaucoup!
bonjour,
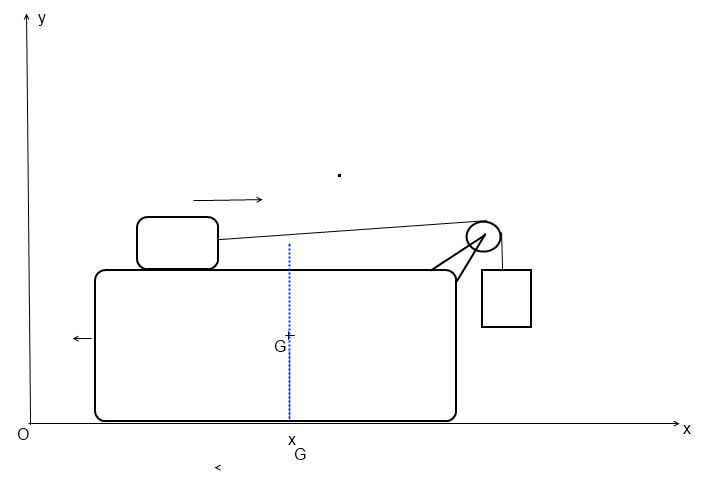
si on considère le système {chariot+masses}, celui-ci n'est soumis à aucune force horizontale si on néglige les frottements. (voir dessin)
on a donc: dPx/dt = 0
Px, la quantité de mouvement selon (Ox), est constante
comme elle est nulle au départ, elle reste nulle durant le mouvement.
Comme la masse de 1kg part vers la droite, le reste du système est obligé de partir vers la gauche pour que Px reste nulle.
(c'est la même chose que pour le patineur qui envoie un ballon devant lui et qui part en arrière)
une autre façon de le voir:
soit xG: abscisse du centre de masse du système {chariot+masses}
on a: mx"G = Fx = 0 donc x'G = cste = 0 (car le chariot est à l'arrêt à t=0)
donc xG reste constant durant le mvt donc comme une des masses part vers la droite, il faut bien que le reste du système parte vers la gauche pour que G garde la même abscisse
sauf erreur
Merci pour ta réponse! Je comprends bien ton explication mais il y a une partie qui me pose soucis.
Comment être sûr que comme le système ne possède aucune force horizontal la quantité de mouvement horizontal est conservée? Quelqu'un a une démonstration ? 



