Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Chien d'euler

Posté par
chorouk 10-10-17 à 20:29

Un Chien (C) est tiré par son maître (M) par l'intérim d'une laisse inextensible de longueur a, toujours tendue. Les mouvements de C et de M ont lieu dans un même plan. A l'instant t=0, M part de l'origine O du repère (O,i,j) et se dirige a la vitesse Vo cte le long de l'axe (O,j) alors que C se trouve en A(x=a,y=0). Déterminer l'équation cartésienne de la trajectoire du chien y=f(x) .

Posté par
vanoisere : Chien d'euler 10-10-17 à 20:55

Bonsoir
Il s'agit d'une des nombreuses version du traditionnel problème de poursuite. Tu trouveras ici une démonstration rigoureuse que tu vas devoir adapter à tes notations.

Posté par
choroukre : Chien d'euler 10-10-17 à 21:44

Merci pour votre intérêt. Merci..!

Posté par
vanoisere : Chien d'euler 10-10-17 à 22:08

Réflexion faite, le problème est tout de même un peu différent du traditionnel problème de poursuite dans lequel le chien court plus vite que son maître.
Ici, la distance CM reste fixe ; en écrivant que le carré de la norme du vecteur \vec{CM} reste fixe, on obtient :

x^{2}+\left(V_{0}.t-y\right)^{2}=a^{2}
D'autre part, et cela n'est pas clairement dit dans ton énoncé, le chien court en permanence en direction de son maître. A chaque instant de date t, le vecteur déplacement élémentaire de :

\overrightarrow{dC}=dx.\overrightarrow{i}+dy.\overrightarrow{j}
est colinéaire au vecteur \vec{CM} :

\overrightarrow{CM}=-x.\overrightarrow{i}+\left(V_{0}.t-y\right).\overrightarrow{j}
Le produit vectoriel de ces deux vecteurs est donc à chaque instant le vecteur nul. Cela va te conduire à une équation différentielle...
Je te laisse continuer...
Cela dit, tu vas devoir calculer une primitive par rapport à x de \frac{\sqrt{a^{2}-x^{2}}}{x}
Cela n'est pas vraiment évident... Franchement, le problème classique de la poursuite est plus intéressant en demandant plus de réflexion physique et moins de mathématiques...

Posté par
vanoisere : Chien d'euler 10-10-17 à 23:02

Selon le Handbook :

\int\frac{\sqrt{a^{2}-x^{2}}}{x}\cdot dx=\sqrt{a^{2}-x^{2}}-a\cdot\ln\left(\frac{a+\sqrt{a^{2}-x^{2}}}{x}\right) \\

Posté par
J-Pre : Chien d'euler 11-10-17 à 10:23

"D'autre part, et cela n'est pas clairement dit dans ton énoncé, le chien court en permanence en direction de son maître. "

C'est parce que, je pense, c'est inutile de le préciser ...

En effet, il est dit que c'est le maître qui TIRE le chien et donc le chien se comporte comme un objet sans vie, comme il est tiré par une corde tendue ... il se dirige donc en permanence vers la position de M

Posté par
diracre : Chien d'euler 11-10-17 à 14:26

Hello J-P

Il faudrait que je te présente mon chien ...  

Posté par
vanoisere : Chien d'euler 11-10-17 à 17:35

Bonjour dirac , Bonjour Chorouk,
Moi aussi j'ai un chien ... Inutile de dire que la précision que j'ai fournie  est plus que nécessaire... D'ailleurs, en consultant d'autres forums, on constate que cet exercice ressort assez régulièrement et que les étudiants bloquent tous de la même façon : ils ne voient pas comment déduire de l'énoncé, tel qu'il est posé, le fait que le vecteur vitesse et le vecteur CM puissent être  colinéaires.
Enfin : puisque JP nous donne l'occasion de faire un peu de physique dans un exercice qui en comporte si peu : imaginons un objet inanimé (un solide) de centre d'inertie C tiré par un fil horizontal sur un plan horizontal, la direction du fil dans le plan horizontal variant au cours du temps. Je suppose pour simplifier les frottements négligeables et l'étude se fait dans le référentiel terrestre supposé galiléen. Dans ces conditions, puisque le poids est compensé par la réaction normale, l'accélération est colinéaire au fil. Or, pour un mouvement curviligne, l'accélération n'est pas colinéaire au vecteur vitesse. Le vecteur vitesse n'est donc pas colinéaire au fil !
On peut aussi imaginer l'existence de frottements solides. En supposant valides les lois de Coulomb correspondantes, cela revient à ajouter à l'accélération une composante suivant (-\vec{V_C} ) de norme constante. J'avoue ne pas avoir fait le calcul complet mais je doute fort que cela conduise à l'accélération du mouvement de C.
Bref : je pense plutôt qu'il faut imaginer un chien suffisamment docile et bien dressé pour orienter à chaque instant sa vitesse suivant la direction de la laisse : totalement irréaliste à mon avis mais il s'agit ici d'un exercice de pensée destiné à familiariser l'étudiant avec la cinétique. Les exercices plus réalistes viendront quand le cours sera plus avancé...

Posté par
choroukre : Chien d'euler 11-10-17 à 20:18

   Merci vanoise , mais je ne sais pas comment developper l'équation différentielle , et aussi je n'ai pas bien compris comment on va avoir  -Vc.
Merci J-p , merci Dirac.

Posté par
diracre : Chien d'euler 11-10-17 à 20:35

Citation :
merci Dirac


Euh ... moi j'ai juste tenté une blague à 2 anciens francs pour suggérer que l'hypothèse du chien qui court vers son maître (le chien d'Euler "original") n'était pas si clair. Je te laisse (tiens, tiens) aux mains de Vanoise et J-P  ...

Posté par
vanoisere : Chien d'euler 11-10-17 à 22:06

Bonsoir chorouk
Je vais essayer de répondre à tes deux questions.
Pour la première : en utilisant la méthode suggérée sur le produit vectoriel, ou tout autre méthode permettant d'exprimer mathématiquement le fait que \vec{CM} et \vec{dC} sont colinéaires ou encore en utilisant la méthode graphique exposée dans le document que je t'ai fourni, tu arrives à :

\left(V_{0}.t-y\right).dx=-x.dy\quad soit\quad\frac{dy}{dx}=-\frac{V_{0}.t-y}{x}

Or, la relation traduisant la conservation au cours du temps de la distance (CM) conduit à :

\left(V_{0}.t-y\right)^{2}=a^{2}-x^{2}

Le vecteur vitesse étant orienté de C vers M en permanence, la vitesse de C à constamment une composante suivant x négative. Le chien avance en se rapprochant de l'axe (O,y). L'angle entre lla laisse et l'axe (O,y), intialement égal à 90° va diminuer au cours du temps jusqu'à devenir nul. Cela implique que, quel que soit t au cours du mouvement étudié :

V_{0}.t-y=y_{M}-y\geq0

De plus : a x. On peut donc poser :

\left(V_{0}.t-y\right)=\sqrt{a^{2}-x^{2}}

D'où l'équation différentielle :

\frac{dy}{dx}=-\frac{\sqrt{a^{2}-x^{2}}}{x}

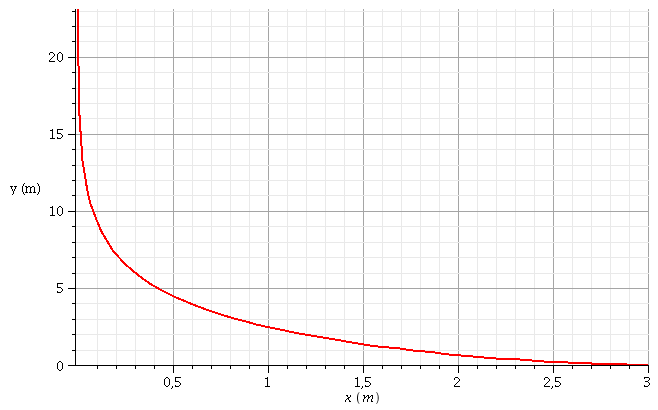
Je te laisse intégrer et terminer... Tu trouveras ci-dessous l'allure de la trajectoire pour a = 3m.

Deuxième questions sur les frottement solide. Dans le contexte décrit dans mon message de 17h35, le glissement d'un solide avec frottement sur un plan horizontal fait que ce solide est soumis à une force de frottement horizontale, orientée suivant la direction et le sens du vecteur \left(-\overrightarrow{V_{c}}\right)et de norme f.Rn où f est le coefficient de frottement et Rn la réaction normale du plan qui compense le poids. L'application de la relation fondamentale de la dynamique au solide fait donc intervenir, en plus d'une accélération colinéaire à CM due à la tension du fil, une accélération supplémentaire colinéaire à (-\overrightarrow{V_{c}}\right). Mais tu n'as sans doute pas, pour l'instant, étudier en cours les lois de Coulomb sur les frottements solides. Contente-toi dans ce cas de bien comprendre pourquoi, en absence de frottement, un solide tiré par un fil dont la direction varie au cours du temps ne peut avoir une vitesse colinéaire au fil à chaque instant. D'où la nécessité d'un chien docile et très bien dressé... ce qui n'est pas le cas de mon chien et de beaucoup d'autres chiens je pense ! En revanche, imagine un lapin qui court animé d'un mouvement rectiligne uniforme. Si tu lâches à ses trousses un bon chien de chasse, tu auras sensiblement (je n'écris pas rigoureusement) la situation modélisée sur le document que je t'ai fourni...

Chien d\'euler

Posté par
choroukre : Chien d'euler 11-10-17 à 23:41

Merci beaucoup Vanoise ...

Posté par
vanoisere : Chien d'euler 12-10-17 à 18:19

Citation :
Merci beaucoup

De rien !
Si tu as un peu de temps devant toi pour approfondir, voici, sauf erreur de ma part, les équations horaires du mouvement de C. Je te laisse vérifier...

\boxed{x=\frac{2a\cdot e^{\frac{Vo.t}{a}}}{1+e^{\frac{2Vo.t}{a}}}=\frac{a}{\cosh\left(\frac{Vo.t}{a}\right)}}

\boxed{y=Vo.t-a\cdot\frac{e^{\frac{2Vo.t}{a}}-1}{e^{\frac{2Vo.t}{a}}+1}=Vo.t-a\cdot\tanh\left(\frac{Vo.t}{a}\right)}

Posté par
J-Pre : Chien d'euler 13-10-17 à 08:59

vanoise extrapole mes propos ...

Je n'ai jamais précisé sans frottement ou autre chose.

Le maître tire le chien ... qui résiste en freinant des quatre fers sur le sol si on veut.

C'est moins loin de l'énoncé d'un chien qui court vers son maître
**********************
Piqué sur le net :

Chien tiré par une laisse ( chien d'euler ? )

Message par mimow » dim. oct. 14, 2012 4:08 pm
Bonjour tout le monde, aujourd'hui j'ai voulu me lancer dans des exo plus durs en ce qui concerne la cinématique du point, et en rencontrant cet exercice, je me suis cogné a quelques difficultés, pour ceux qui ne connaissent pas cet exercice :

Un Chien (C) est tiré par son maître (M) par l'intérim d'une laisse inextensible de longueur a, toujours tendue. Les mouvements de C et de M ont lieu dans un même plan. A l'instant t=0, M part de l'origine O du repère (O,i,j) et se dirige a la vitesse Vo cte le long de l'axe (O,j) alors que C se trouve en A(x=a,y=0). Déterminer l'équation cartésienne de la trajectoire du chien y=f(x) .

Après pas mal d'essais et de réflexion je me suis résigné à voir la solution de l'exercice et là j'ai trouvé les 2 clefs de l'exercice dont une que j'avais découvert avant mais qui est insuffisante sans l'autre.
SPOILER:
* La laisse restant tendue, la distance entre le chien et le maître reste cte est égale "a" soit: x² + (Vo *t -y)² = a²
* Le maître oblige le chien a se déplacer vers lui en tirant constamment sur la laisse : Le déplacement élémentaire dOC = dx * i + dy * j ( expression vectorielle )
du chien est à tout instant colinéaire au vecteur CM = -x * i + (Vo*t - y ) * j .
On peut donc écrire : -dx/x = dy/(Vo*t - y), d'ou Vo*t - y +x(dy/dx)=0

Je suis d'accord à 100 % avec ce point de vue.

Posté par
vanoisere : Chien d'euler 13-10-17 à 11:21

message du 11-10-17 à 10:23 :

Citation :
donc le chien se comporte comme un objet sans vie

message du 13-10-17 à 08:59
Citation :
Le maître tire le chien ... qui résiste en freinant des quatre fers sur le sol

???

Posté par
J-Pre : Chien d'euler 13-10-17 à 11:37

Ben oui.

Le maître oblige le chien a se déplacer vers lui en tirant constamment sur la laisse ... ce n'est pas "le chien court vers son maître"

Remarque que la solution du problème MODIFIE avec le chien qui court vers son maître en gardant la laisse tendue aboutit à la solution sans aucun doute attendue... mais c'est quand même un énoncé modifié...
Et je suis aussi d'accord avec la remarque que l'énoncé primitif aurait pu être écrit un peu autrement pour éviter les interprétations hasardeuses.

Posté par
choroukre : Chien d'euler 22-10-17 à 22:00

Merci ,, mais comment obtenir les équations horaires du mouvement de C depuis l'équation de la trajectoire .

Posté par
vanoisere : Chien d'euler 22-10-17 à 22:22

Bonsoir
Partant de l'équation de la trajectoire :

y=a.\ln\left(\frac{a+\sqrt{a^{2}-x^{2}}}{x}\right)-\sqrt{a^{2}-x^{2}}

tu remplaces \sqrt{a^{2}-x^{2}}  par \left(V_{0}.t-y\right)

Tu obtiens alors  \ln\left(\frac{a+\sqrt{a^{2}-x^{2}}}{x}\right)
  en fonction de t,a et Vo. Il suffit alors de passer à l'exponentielle...
Il est aussi possible de remarquer :

a.\ln\left(\frac{a+\sqrt{a^{2}-x^{2}}}{x}\right)=a.Arctanh\left(\frac{\sqrt{a^{2}-x^{2}}}{a}\right)

Posté par
choroukre : Chien d'euler 22-10-17 à 23:55

oui , mais il y'a un problème l'intégrale de la racine (1-x^2)/x n'est pas vraie

Posté par
J-Pre : Chien d'euler 23-10-17 à 10:21

chorouk @ 22-10-2017 à 23:55

oui , mais il y'a un problème l'intégrale de la racine (1-x^2)/x n'est pas vraie


Que veux-tu dire par là ?

S V(1-x²)/x dx = S x.V(1-x²)/x² dx

Poser 1-x² = z² --> x dx = -z dz

S V(1-x²)/x dx = - S z²/(1-z²) dz = -1/2 * [S z/(1-z) dz - S z/(1+z) dz]
= -1/2 * [S (z-1+1)/(1-z) dz - S (z+1-1)/(1+z) dz]
= -1/2 * [- S dz + S dz/(1-z) - S dz + S dz/(1+z)]
= S dz + (1/2) S dz/(z-1) - 1/2 S dz/(1+z)]
= z + (1/2).ln|z-1| - 1/2.ln|z+1|

S V(1-x²)/x dx = V(1-x²) + (1/2).ln|V(1-x²) - 1| - (1/2).ln|V(1-x²) + 1|

Et donc F(x) = V(1-x²) + (1/2).ln|V(1-x²) - 1| - (1/2).ln|V(1-x²) + 1| est UNE primitive de f(x) = V(1-x²)/x

Sauf distraction.  

Posté par
diracre : Chien d'euler 23-10-17 à 12:46

Ben je me coucherai moins bête ce soir ...

1) j'ai compris les notations de J-P  

2) je viens surtout de comprendre ce qui me tracassait depuis qlq jours: la restitution de x(t) et de y(t) par Vanoise qui donnait d'abord les fonctions exponentielles de t puis les fonctions hyperboliques, tandis que la résolution des équations différentielles donnaient plutôt d'abord les solutions en th et ch, =>  la détermination de la trajectoire puis la réintégration de y(t) dans l'équation cartésienne est plus économe en calculs, donc réduit le risque d'erreur  (à avoir en tête pour une prochaine fois)  

Posté par
vanoisere : Chien d'euler 23-10-17 à 15:42

Bonsoir Dirac

Citation :
j'ai compris les notations de J-P    

Bravo !
Bonsoir chorouk
Citation :
il y'a un problème l'intégrale de la racine (1-x^2)/x n'est pas vraie

Tu sais : le "Handbook of Chemistry and Physics" est vraiment le livre de référence de tous les chercheurs et enseignants du monde. Je crois bien qu'on le trouve dans tous les bureaux de recherche ! Cela dit : j'aurais pu commettre une faute de frappe !
Voici une démonstration possible donnant une expression de la primitive faisant intervenir directement la fonction arctangente hyperbolique inverse. Réflexion faite : l'obtention des équations horaires est un peu plus simple ainsi.
Je pose :

P=\int\frac{\sqrt{a^{2}-x^{2}}}{x}\cdot dx

Changement de variable : je pose :

u=\sqrt{a^{2}-x^{2}}

\frac{du}{dx}=-\frac{x}{u}\quad;\quad dx=-\frac{u}{x}.du

\frac{\sqrt{a^{2}-x^{2}}}{x}\cdot dx=-\frac{u^{2}}{x^{2}}.du=-\frac{u^{2}}{a^{2}-u^{2}}.du=\frac{a^{2}-u^{2}-a^{2}}{a^{2}-u^{2}}.du=du-\frac{a^{2}}{a^{2}-u^{2}}.du

Donc :

P=u-\int\frac{a^{2}}{a^{2}-u^{2}}.du=u-F\quad avec\quad F=\int\frac{a^{2}}{a^{2}-u^{2}}.du

Dernier changement de variable : v=\frac{u}{a}

dv=\frac{du}{a}\quad;\quad\frac{a^{2}}{a^{2}-u^{2}}=\frac{1}{1-v^{2}}

F=a.\int\frac{dv}{1-v^{2}}=\frac{a}{2}.\left[\int\frac{dv}{1+v}+\int\frac{dv}{1-v}\right]=\frac{a}{2}.\ln\left(\frac{1+v}{1-v}\right)=a.\text{arctanh\ensuremath{\left(v\right)=a.\text{arctanh\ensuremath{\left(\frac{u}{a}\right)}}}} \\
D'où le résultat final :

P=u-a.\text{arctanh\ensuremath{\left(\frac{u}{a}\right)}}

P=\int\frac{\sqrt{a^{2}-x^{2}}}{x}\cdot dx=\sqrt{a^{2}-x^{2}}-a.\text{arctanh\ensuremath{\left(\frac{\sqrt{a^{2}-x^{2}}}{a}\right)}}

Remarque : le passage du logarithme à l'arctangente hyperbolique est un classique des cours de maths. Démonstration possible ici :

Remarque complémentaire : si on conserve le logarithme sans faire intervenir la fonction tangente hyperbolique, le calcul précédent conduit à :

P=\int\frac{\sqrt{a^{2}-x^{2}}}{x}\cdot dx=\sqrt{a^{2}-x^{2}}-\frac{a}{2}.\ln\left(\frac{a+u}{a-u}\right)=\sqrt{a^{2}-x^{2}}-\frac{a}{2}.\ln\left(\frac{a+\sqrt{a^{2}-x^{2}}}{a-\sqrt{a^{2}-x^{2}}}\right)

Est-ce bien une expression équivalente à celle fournie par le Handbook ?

Selon le handbook :

P=\int\frac{\sqrt{a^{2}-x^{2}}}{x}\cdot dx=\sqrt{a^{2}-x^{2}}-a\cdot\ln\left(\frac{a+\sqrt{a^{2}-x^{2}}}{x}\right)

Or :

\ln\left(\frac{a+\sqrt{a^{2}-x^{2}}}{x}\right)=\ln\left(\frac{a+u}{\sqrt{a^{2}-u^{2}}}\right)=\ln\left(\frac{a+u}{\sqrt{a+u}\cdot\sqrt{a-u}}\right)=\ln\left(\frac{\sqrt{a+u}}{\sqrt{a-u}}\right)=\frac{1}{2}.\ln\left(\frac{a+u}{a-u}\right)=\frac{1}{2}.\ln\left(\frac{1+v}{1-v}\right)

Pas de problème donc, au moins dans la mesure où : 0<x\leq a

Posté par
vanoisere : Chien d'euler 23-10-17 à 19:04

L'habitude  de la notation "arctanh(x)" pratiqué par certains logiciels anglo-saxons m'a fait parler d'arctangente hyperbolique plutôt que d'argument tangente hyperbolique...
Je présente mes plus plates excuses pour cette  erreur de langage mais je ne pense pas que cela puisse affecter la compréhension !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !