Inscription / Connexion Nouveau Sujet
Charges ponctuelles au sommets d'un carré ABCD
Bonjours,
Mon exercice est le suivant:
On place 4 charges ponctuelles aux sommets ABCD d'un carré de côté a=1m, et de centre O, origine d'un repére Oxy de vecteurs unitaires 
et 
. On donne q1=q; q2=-2q; q3=2q; q4=-q.
1) Déterminer le champ électrique 
au centre O du carré. Préciser le sens et la norme de ce champ.
2)Exprimer le potentiel V créé en O par les 4 charges.
3)Exprimer le potentiel sur les parties des axes x'x et yy' intérieures au carré. Quelle est, en particulier, la valeur de V aux points d'intersection de ces axes avec les côtés du carré(I,I',J et J')?
1) est selon par raison de symétrie.
Calculons sa norme:
E1+E4=-(q/4
0) *cos(/4)*2*OE1. Après je bloque
Bonjour,
Pour la direction du vecteur champ, j'ignore ce que tu appelles : je ne peux donc pas confirmer ta réponse.
Tu peux exprimer chacun des quatre vecteurs champ et projeter sur l'axe (O,).
N'ayant pas de figure, j'ai supposé que q1 est en A, q2 en B, q3 en C et q4 en D. Si ce n'est pas le cas, tu devras adapter la méthode.
Il y a cependant plus rapide. De façon générale, une charge q centrée en un point P crée en un point M un champ de vecteur :
Dans ton problème, les quatre charges sont à la même distance r du centre O :
De façon immédiate, le vecteur champ total en O a pour vecteur :
Il y a des simplifications possibles puisque la norme du vecteur CB vaut a...
Merci.
A la fin, je trouve E=(qa/40*(a/
2)[sup][/sup]3) en norme et pour le potentiel je trouve 0. Ensuite, je ne sais pas trop comment m'y prendre.
Ta formule est totalement illisible !
Cela devrait donner :
Un point M sur l'axe (Ox) a pour coordonnées (x,0) ; les coordonnées des sommets sont faciles à obtenir. Les distances de M aux quatre sommets sont alors faciles à exprimer en fonction de x et a : se sont les normes des vecteurs AM, BM, CM et DM.
Merci beaucoup pour ton aide. Bonne année à tous.
La seul chose sur laquelle on n'est pas tombé d'accord, c'est la valeur de r.
cos(/4)=(a/2)/r
Donc r=(a/2)/cos(/4 donc r=(a/2)/(2/2).
Alors r=2.a car chaque côté du carré fait une longueur a.
Donc au final, je trouve: E=q2/(40.a2).
Après pour la 2, j'ai trouvé: V=0. Par contre pour la 3, je ne sais pas trop comment m'y prendre.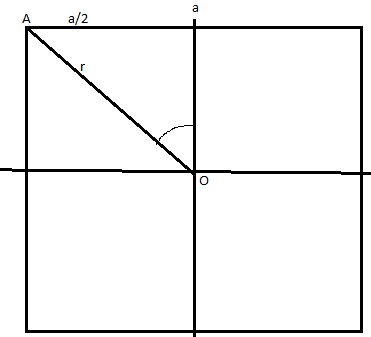
***Image recadrée***
Bonjour,
Selon toi : r =a2 soit r 1,4 fois plus grand que a environ : cela te paraît réaliste ?
Pour la suite : je t'ai déjà donné quelques indications ; j'en rajoute une couche en utilisant les coordonnées des points dans ton repère.
Soit M(x,0) ; A(-a/2,a/2). Le vecteur AM a pour composantes : -(a/2 - x),(-a/2) ; la distance AM est donc :
Tu fait de même pour les distances de M aux autres sommets du carré et tu en déduis le potentiel.
Même méthode ensuite si M(0,y)...
Bonjour,
J'ai le même exercice à faire. J'ai donc suivis votre méthode avec le M(x;0) et M(0;y). Seulement, je trouve au lieu de
d'après mon énoncé. Je ne sais pas où est mon erreur
Bonjour
Je suis d'accord avec ton résultat. Alors : erreur de ton corrigé ou notations différentes ? Es-tu bien sûr que les charges et leurs dispositions sont bien identiques dans les deux problèmes ?
J'ai pris avec mes valeurs, c'est-à-dire q1=q, q2=-2q, q3=2q et q4=-q avec q1 en A, q2 en B, q3 en C et q4 en D pour un carré ABCD. Il est possible que l'énoncé soit faux alors ?
Pour V en J, j'ai trouvé
et V en J' :
Est-ce bien cela ? Si oui, j'obtiens une valeur négative pour le potentiel en J. Je ne me souviens plus, on peut obtenir un potentiel négatif ?
vanoise
Bonjour à vous deux,
@Meg09 : merci de régulariser urgemment ta situation en supprimant ton compte Meghanou (ou celui que tu utilises actuellement). Pour mémoire :
la FAQ du forumLe corrigé est effectivement faux s'il place les charges comme tu l'as indiqué et si l'axe Oy est bien la médiatrice des segments (AB) et (DC) avec une origine O au centre du carré. L'expression du potentiel créé en M par les quatre charges s'écrit :
Quand M est sur l'axe des ordonnées : AM=BM et CM=DM ; donc :
Or :
Cela conduit à l'expression que tu as fournie, pas à celle de ton corrigé qui est manifestement fausse.
D'accord avec tes calculs. Tu pourrais sans doute les simplifier pour ne pas laisser une racine carrée au dénominateur.
Ici, le potentiel zéro est choisi arbitrairement infiniment loin des charges. Ainsi, une charge positive créé un potentiel positif à distance finie, une charge négative crée un potentiel négatif à distance finie. La superposition des potentiels créé par plusieurs charges, certaines positives, certaines négatives, peut donc voir son signe changer en fonction des distances du point M aux différentes charges...
Annuler
connectez vous