Inscription / Connexion Nouveau Sujet
charges électriques aux sommets d'un triangle équilatéral
Bonjour,
Je n'arrive pas à voir comment expliquer géométriquement que le champ est orienté vers le centre O en dessinant les composantes de chacun des 3 champs (du aux 3 charges!), merci de votre aide
Un triangle équilatéral ABC, inscrit dans un cercle (C) de centre O et de rayon R, possède sur chacun de ses sommets une charge ponctuelle négative q.
L'axe x'Ox d'origine O et de vecteur unitaire ex est perpendiculaire au triangle ABC.
Un point M appartenant à x'Ox est défini par son abscisse x
On se place dans le vide, de permittivité diélectrique epsilon0, et le potentiel électrique est supposé nul à l'infini.
1. Ecrire le potentiel électrique V(M) au point M en fonction de x.
je somme les 3 potentiels crée par les 3 charges et j'obtiens : V(M)= 3qK/sqrt(R2 + X2)
2. Dessiner et exprimer le champ électrique au point M.
L'expression du champ n'est pas compliqué en passant par le gradient (E = 3qkx/(R2+X2)3/2, mais pour l'expliquer géométriquement et le dessiner je bloque!
D'accord avec tes résultats.
La représentation des trois vecteurs champ créés par les trois charges n'est pas évidente puisqu'il faut faire une figure en 3D.
Tu pourrais commencer par vérifier géométriquement que E=0 en x=0 (M confondu avec O).
Pour x différent de zéro, tu pourrais commencer par représenter une pyramide à base triangulaire (le triangle ABC) et de sommet M. N'hésite pas à scanner et poster ton schéma ici. Les trois vecteurs champ sont colinéaires à MA, MB et MC et le vecteur champ résultant est colinéaire à MO. N'oublie pas : q<0 !
Merci Vanoise pour ta réponse.
Le champ crée par les charges placées en A et B est de M vers le centre de [AB], est ce qu'on peut trouver l'angle entre ce vecteur et l'axe Ox?
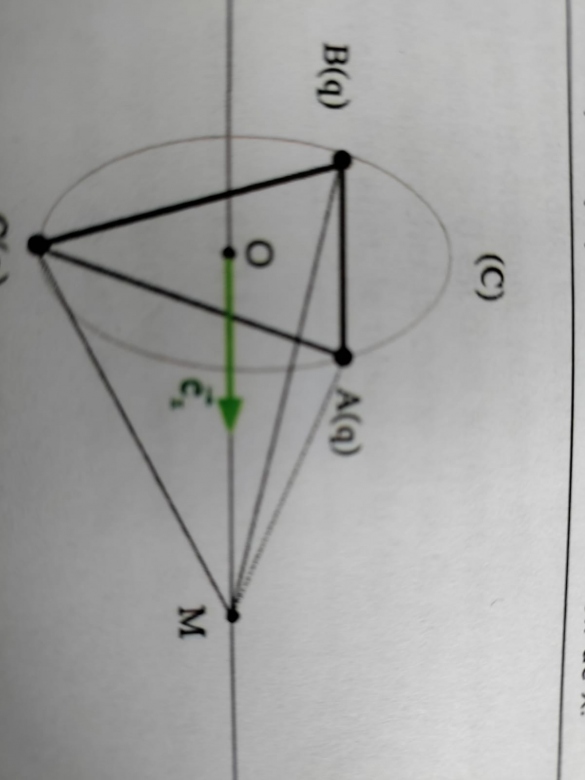
Il faut représenter les trois vecteurs champ à partir du point M où on étudie le champ. Voir ci-dessous l'exemple du vecteur champ créé en M par la charge q centrée en C. Pour trouver la direction du vecteur champ, on peut raisonner sur les plans de symétrie. On peut aussi partir de la loi de Coulomb écrite sous cette forme :
Puisque les trois distances AM, BM et CM sont égales :
Je te laisse démontrer que la somme des trois vecteurs entre parenthèse est un vecteur colinéaire à .
Tu pourras en plus vérifier la cohérence de ce résultat avec celui que tu as obtenu à partir du gradient du potentiel en M.
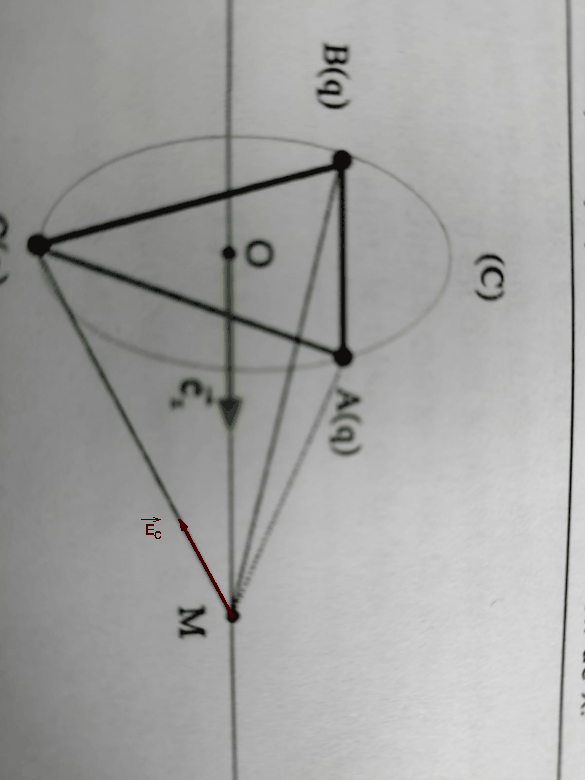
Oui, je vois ce que tu suggères, décomposer les vecteurs (Chasles), mais c'est une réponse analytique et non géométrique.
Tu peux ”ruser” un peu... Chaque vecteur champ est la somme d'un vecteur colinéaire à OM et d'un vecteur colinéaire à AO ou BO ou CO. Les composantes selon OM s'ajoutent ; la somme des composantes dans le plan du triangle est le vecteur nul. Tu peux déduire cela de la relation vectorielle :
mais tu peux aussi le montrer géométriquement en traçant les représentant des trois vecteurs champs appartenant au plan du triangle.
Bonsoir à tous les deux,
khalidou67, pourrais-tu avoir la politesse d'aller dire sur futura que tu n'as plus besoin d'aide...car poster ainsi en parallèle n'est pas fort respectueux de ceux qui t'aident
Bonsoir mmalou
Merci pour ta vigilance. Tu as remarqué j'imagine toi aussi que l'histoire se répète...
Bonjour mmalou,
Si j'ai posté sur les deux forums c'est dans le but d'avoir des idées différentes, et pour l'instant (merci vanoise) je n'ai pas eu une réponse géométrique à la question posée........en quoi cela est irrespectueux?
euh et c'est quoi ça ?
mais tu peux aussi le montrer géométriquement en traçant les représentant des trois vecteurs champs appartenant au plan du triangle.
Ok, je ne savais pas que sur deux sites différents on pouvait assimilé cela à du multi-post.
Merci de votre aide.
Merci d'avoir mis un mot chez futura.
Maintenant tu peux terminer avec vanoise si tu as encore des questions.
Bonne journée
La géométrie... Tu ne peux pas faire une démonstration qui évite de faire un peu de physique et d'utiliser les expressions des vecteurs champ. Il te faut donc passer par les relations déjà écrites :
Puisque les trois distances AM, BM et CM sont égales :
Facile alors en représentant les vecteurs de montrer géométriquement :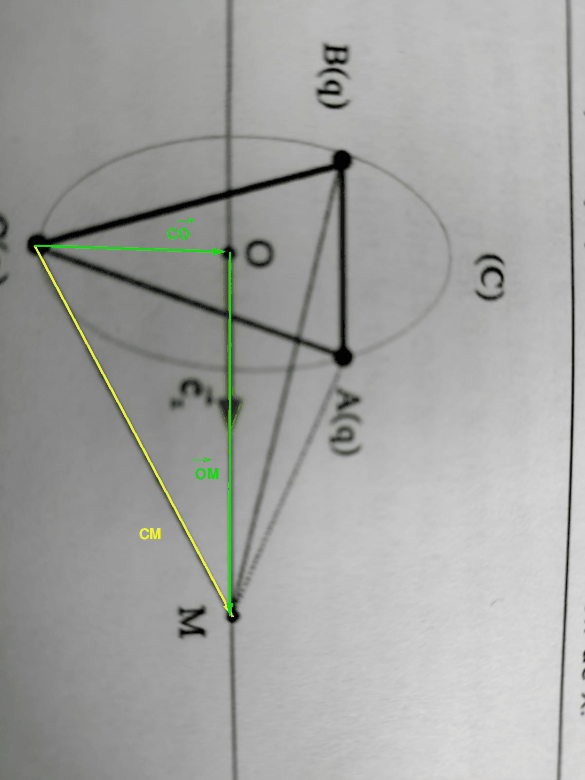
**malou edit > balises Ltx ajoutées**
Je viens de relire l'énoncé tel que tu l'as copié. Cet énoncé n'exige pas un raisonnement "géométrique". Il s'agit juste d'établir l'expression du vecteur champ : cela est immédiat par la méthode que j'ai proposée le 29-09-21 à 12:15 et on demande ensuite de tracer un représentant du vecteur champ : il suffit de tracer un vecteur à partir du point M colinéaire à puisque q<0.
Autre remarque : déduire l'expression du vecteur champ en M de l'expression du potentiel en M comme tu l'as fait n'est rigoureux que si tu démontres au préalable que le vecteur champ est colinéaire à . Outre la méthode déjà indiquée qui fournit aussi l'expression du vecteur champ en M, tu peux t'intéresser aux plans de symétrie de la source du champ qui contiennent le point M. C'est la méthode la plus habituelle pour déterminer la direction d'un vecteur champ sans le moindre calcul.


 ) :
) :

