Inscription / Connexion Nouveau Sujet
changement de référentiel,mouvements complexes.
Bonjour!
Voici mon problème: j'ai un exercice à rendre en mécanique dans deux jours... Ne croyez pas que je m'y met que maintenant, j'ai essayé de comprendre cet exercice, mais j'ai beaucoup de doute. Je ne sais pas comment m'y prendre, sûrement n'ai-je rien compris au cours :/ .
^^" il me reste que deux jours, mais comme j'aimerais comprendre, je vais quand même essayé deux exercices qui ressemble à celui que je dois rendre, (trouvé sur internet) avant d'attaquer ce dernier.
Les deux exercices d'essais : (tous les schémas sont en dessous)
EXERCICE 1 ** exercice effacé **
EXERCICE 2 ** exercice effacé **
EXERCICE A RENDRE:
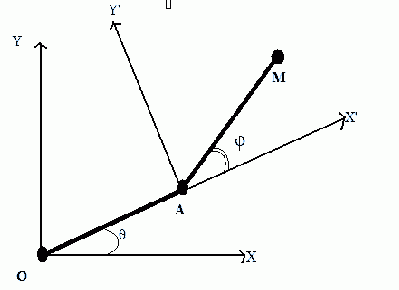
Deux barres de fer de longueur l sont fixées en A. La première, représentée par OA, est en rotation autour du point O dan le plan (O,x,y) avec une vitesse angulaire 
(=cte). La seconde, représentée par AM, décrit un cercle de centre A avec une vitesse angulaire 1(1=cte). A l'instant initial, les points O,A et M sont alignés sur l'axe Ox.
1.Déterminer le vecteur position de M dans Oxy en fonction de l, 
et 
.
2.Calculer directement les vecteurs vitesse et accélération de M dans Oxy en fonction de l,,1 et .
3.On se place dans le cas ou =1=.t
a.Exprimer le vecteur position et les vecteurs vitesse et accélération de M dans (O,x,y) en fonction de l, et .
b.Exprimer la vitese et l'accélération relatives dans Oxy en fontion de l, et .
c.Exprimer la vitesse et l'accélération d'entrainement dans Oxy en fonction de l, et ? On utilisera la méthode du point coïncident?
d.En déduire l'accélération complémentaire dans Oxy.
e.Démontrer que 
e=dvect(OA)/dt +vect()^vect(AM)
vect(ac)=2*vect()/r
*** message dupliqué ***
Edit Coll : topic dupliqué ; merci de respecter la FAQ, un problème = un topic 
[lien]
Bon! pr le petit 1:
j'ai trouvé:
v(OA) dans Oxy= lcos(t)
+lsin(t)
v(AM) dans Ax'y'=lcos(1t)+lsin(1t)
ce qui me donne
v(OA) dans Oxy= l[ (cos(t)+1/2(cos([1t-t)+cos(1t+t)))vecti[/smb]+sin(t)]
Est-ce correct?
Bonjour, pour les vecteurs positions, il faut projeter sur les axes x et y.
Pour les vecteurs vitesses il faut dériver les vecteurs positions.
Enfin pour l'accélération il faut dériver les vecteurs vitesses.
Ok...c'est plus bête que ce que je m'imaginais :/
( v(OA) <=> vect(OA) <=> vecteur(OA) dans mes post précédents .... je crois que j'avais la flemme d'écrire vect... lol)
le vect(OM) c'est plutôt 'en fonction de l, et )
vect(OM)= l*[cos()+cos(+) ) + sin()+sin(+).
ce qui fait que vect(VOM)= d/dt(vect(OM))
vect(VOM)=l*(-sin()-(+1)sin(+) ) + (cos()+(+1)cos(+) ) )
et donc que vect(aOM)=
[l((-²cos()-(+1)²cos(+)) +(-²sin()-(+1)²sin(+)))]
n'y a t'il pas un soucis dans le petit 3?
=1=t???
je crois que =t puisque et 1 sont sensés être des constantes d'après l'énoncé...
je continue comme si je n'avais pas fait attention...
3.a) on a:
vect(OM)= l*[(cos()+cos(2))+(sin()+sin(2))]
vect(VOM)= l*[(-sin()-2sin(2))+(cos()+2cos(2))]
et vect(aOM)=l*[(-²cos()-4²cos(2))+(-²sin()-4²sin(2))]
vecteur vitesse et accélération relative dans Oxy
Vect(Vr)=vect(VAM)
Vect(Vr)=l[-2sin(2)+2cos(2)];
vect(ar)=d/dt[Vect(Vr)]
vect(ar)=-4l²(cos(2)+sin(2)
ça ne fonctionne pas! quand j'arrive au bout de l'exercice j'ai tout faux!
il aurait fallut que j'utilise i' et j' sûrement pour Ve et Vr...peut-être aussi pour vect(VOM)???
Mais on me demandetout cela dans Oxy!!!
je suis perdue!
Bonjour,
Concernant le vecteur position du point M dans Oxy, on a je pense :
)
+ l \cdot cos() + l \cdot sin() + l \cdot sin() " alt="\vec{OM} = l \cdot cos() + l \cdot cos() + l \cdot sin() + l \cdot sin() " class="tex" />
Ce qui donne :
)
+ cos() + l \cdot ( sin() +
\\ sin() )" alt="\vec{OM} = l \cdot ( cos() + cos() + l \cdot ( sin() +
\\ sin() )" class="tex" />
Ensuite le vecteur vitesse dérive du vecteur position par rapport au temps:
= l(cos
+ cos ) + l(sin+sin)
Avec = . t
Selon les règles de trigonométrie et le schéma je dirais. Il faudrait que quelqu'un confirme.
Annuler
connectez vous