Inscription / Connexion Nouveau Sujet
changement de référentiel,mouvements complexes.
Bonjour!
Voici mon problème: j'ai un exercice à rendre en mécanique dans deux jours... Ne croyez pas que je m'y met que maintenant, j'ai essayé de comprendre cet exercice, mais j'ai beaucoup de doute. Je ne sais pas comment m'y prendre, sûrement n'ai-je rien compris au cours :/ .
^^" il me reste que deux jours, mais comme j'aimerais comprendre, je vais quand même essayé deux exercices qui ressemble à celui que je dois rendre, (trouvé sur internet) avant d'attaquer ce dernier.
Les deux exercices d'essais : (tous les schémas sont en dessous)
EXERCICE 1
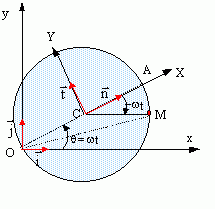
Dans un plan Oxy un cercle de diamètre OA tourne à la vitesse angulaire constante w autour du point O. On associe au centre du disque deux axes rectangulaires CX et CY. A t= 0 le point A est sur Ox et un point M initialement en A parcourt la circonférence dans le sens contraire au sens trigonométrique avec la vitesse angulaire w.
1. Exprimer les composantes des vecteurs vitesse et accélération de M dans le repère Oxy.
2. Exprimer les composantes des vecteurs vitesse et accélération de M dans le repère CXY.
3. Déterminer les expressions de la vitesse d'entraînement et l'accélération complémentaire.
EXERCICE 2 ** exercice recopié dans un nouveau topic et effacé **
EXERCICE A RENDRE : ** exercice recopié dans un nouveau topic et effacé **
Edit Coll : merci de respecter la FAQ, un problème = un topic 
[lien]
Le premier exercice à été pris ici:
le second ici:
Pour l'exercice 1:
Voici comment j'ai procédé:
R(O,x,y) R'(O,x',y').
vect(OM)=vect(OC)+vect(CM):
en coordonnée cartésienne on a:
v(OC)(dans R): OC(cos(wt)
+ sin(wt)
)
v(CM)(dans R'): CM(cos(-wt)'+ sin(-wt))
donc OM= OC(cos(wt)+ sin(wt)) + CM(cos(-wt)'+ sin(-wt)')
on a '= cos(wt)+ sin(wt)
donc OM= OC(cos(wt)+ sin(wt)) + CM(cos(-wt)[(cos(wt)+ sin(wt)]+ sin(-wt)[(sin(wt)- cos(wt)])
<=>OM= OC(cos(wt)+ sin(wt)) + CM(-cos(wt)[(cos(wt)+ sin(wt)]+ sin(wt)[(sin(wt)+ cos(wt)])
Au final je trouve OM= [OC*cos(wt)-CMcos(2wt)]+[OC*sin(wt)-CM*sin(2wt)]
Or avec la correction donné sur le site où j'ai pris le premier exercice, je devrais avoir:
v(OM) = R(1+cos (wt)+ R sin (wt)
Ce que je ne trouve pas, même avec OC=CM ...
rq: même avec le schéma de l'exercice 1, je ne comprend pas le résultat que je devrais avoir, étant donné que le M du schéma est un point qui devrait changé de position à chaque instant t :/
C'est sûr que c'est un peu embêtant à lire 
je viens de remarquer que wt et -wt valent un même angle (je me comprend, mais je ne sais pas trop pour les autres ^^")et donc CM est toujours parallèle à Ox.... (oui oui, je ne l'avais pas vu lol)
Mais c'est quand même bizarre de ne pas trouver le même résultat en exprimant i' et j' en fonction de i et j (les vecteurs)
je vais réessayer, pour voir si je n'aurais pas fait d'erreur...
dans tout les cas, apparemment on peut faire tout simplement:
vect(CM)= CM cos(wt-wt) + CM sin(wt-wt)
ce qui revient à vect(CM) = CM
ce qu'il fallait trouvé...
Si ça marche comme ça, pourquoi ce casser la tête. Je n'avais pas compris qu'on pouvait réellement se fier à l'image, alors qu'il s'agit en réalité de représentation fixe de quelque chose en mouvement.
Quand je dit :
(j'avais oublié la flèche)
Ca equivaux à ta formulation :
v(OC)(dans R): OC(cos(wt)+ sin(wt))
Sauf que je fais par étape pour que tu comprenne.
Mais ce n'est pas vrai pour le vecteur . qui est dèjà sur
.
(Désolé pour le multi post mais on n'a pas editer ou je ne l'ai pas vu)
Pour l'accéleration :
Il faut dériver la vitesse
ce qui donne :
(
c'est la dérivé de w)
pour l'acceleration :
(c'est la dérivé de w)
Pour la partie 3 je te laisse faire car ça ne me dit pas grand chose (je les connais surement sous une autre appellation.
Merci Kryzen!
oui la partie 3 c'est pas compliquer...c'est bête mais vraiment je crois que j'avais juste du mal pour le début ^^"
je reviendrai plus tard
Annuler
connectez vous