Inscription / Connexion Nouveau Sujet
Changement de référentiel
Bonsoir,
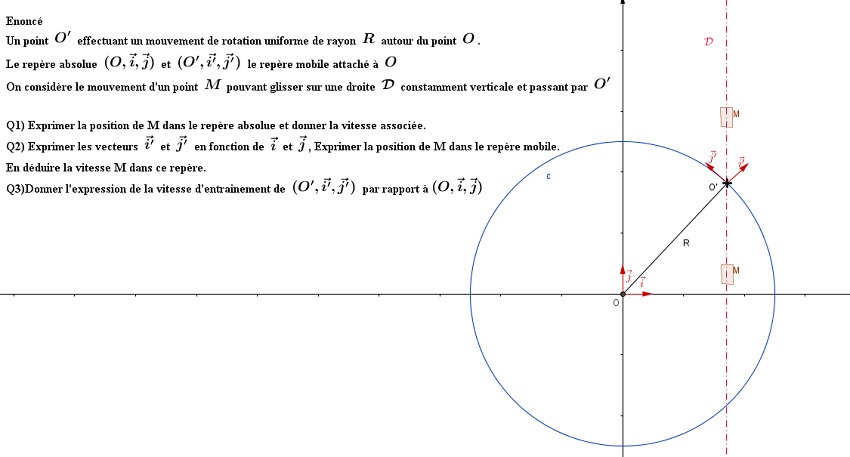
Voici un problème que je trouve ardu et voici mes réponses.( Je n'arrive pas à placer l'image en tête de page) vous trouverez donc l'énoncé en bas de la page.
Question 1
Pour la suite du problème je vais poser et
et que le mobile se déplace à une vitesse
sur l'axe verticale
Position de M dans le repère absolue
La vitesse dans
Mon problème est que je ne sais pas si je dois tenir compte du déplacement du mobile sur l'axe vertical
Question 2
en fonction de
Position du point par rapport à
Vitesse du point par rapport à
Là je suis un peu perdu, et je n'ai pas l'impression, que les expressions soient justes ou alors les expressions de la position et de la vitesse sont mal posées.
Pouvez-vous m'apporter de l'aide s'il vous plait
Je vous remercie
Mousse
Hello
Il y a du bien dans ce que tu écris et puis il y a un peu de confusion je crois ...
Donc cela revient à définir r' et Vv comme:
et
Tu écris
Donc va "droit au but":
Donc
hum, pas tout à fait ...
On sait que
et que, si pour passer de
pour passer de
Tu reprends la main à partir de là?
Bonjour Dirac et merci
Je reprends le relais à partir de là, pas de problème.
Par contre cee sera seulement en fin d'après midi vers 17h. J'ai un programme chargé.
Merci et à trés bientôt.
Bonsoir,
Voici mes corrections :
I) EXPRESSION DE M DANS LE REPERE ABSOLUE ET VITESSE ASSOCIEE :
II) EXPRESSION de EN FONCTION DE
III) EXPRESSION DE M DANS LE REPERE MOBILE ET VITESSE ASSOCIEE :
or
puisque
III) EXPRESSION DE LA VITESSE D'ENTRAÎNEMENT :
IV) CONCLUSION:
Je pense que c'est bon....
Pas tout à fait ...
Je te propose de partir de:
Et de dériver pour trouver
Je te rappelle l'expression usuelle de la composition des vitesses:
PS:
1) tu auras noté que je ne pose pas , il n'est dit nul par dans l'énoncé que la vitesse le long de la droite était constante. Et d'ailleurs cela ne change pas le calcul
2) C'est chouette de lire du Latex aussi bien écrit 
Bonjour dirac,
Merci dirac, pour tes commentaires. Pur le latex, je me balade de temps en temps sur le forum iles des maths
Je voulais dériver en premier mais comme j'ai un vecteur radial et orthoradial à dériver, (et qu'il était tard
 Je me suis dit pourquoi ne pas dériver
Je me suis dit pourquoi ne pas dériver et ensuite effectuer une rotation de
Peux-tu m'expliquer pourquoi on ne peut pas procéder ainsi??
Je viens de me lever, donne moi une heure et ensuite je dérive :
Si je veux la dérivé par rapport au temps puisque :
Suffit de dériver
Et là je me retrouve
Même en sachant que et en ayant dérivé
, je suis bloqué, et complétement perdu...
Veux tu encore te reposer un petit peu? Tu en as visiblement besoin ... (non, là je te "chambre" un petit peu ... trop sans doute  )
)
je dérive par rapport à
 euh pour la vitesse il faut dériver par rapport au temps
euh pour la vitesse il faut dériver par rapport au temps 
Comme r' ne dépend pas de \theta
Une chose est sûr r' dépend de t


Donc, nous avions
Ce qui donne (je vais quand même travailler un peu)
Soit
Tu reprends la mains arrivé là?
Au fait:
Peux-tu m'expliquer pourquoi on ne peut pas procéder ainsi??
Parce que dans le référentiel R',
 est mobile, donc tu n'avais pas le droit d'écrire
est mobile, donc tu n'avais pas le droit d'écrire

Allez tu y es presque!!! et l'expression tant convoitée
Va tomber toute seule

Oui, tu as raison, je vais faire une pause. j'aime pas trop tout ce qui tourne, ça me donne le vertige  .
.
Mais avant, lorsqu'on dérive par rapport au temps une expression qui est fonction de , ne faut-il pas dériver ces vecteurs.
par exemple
Ou alors, comme c'est une vitesse dans le repère , les vecteurs
sont fixes. Est-ce la raison?
Merci pour ton aide
FIAT LUX  TU AS TOUT COMPRIS!!!!
TU AS TOUT COMPRIS!!!!
R' est un REFERENTIEL et pas seulement un repère ...
Bon tu te reposes 5 mn et tu termines?
Juste une autre question :
puisque est fonction
, et que
est fonction de
J'imagine qu'une rotation de s'impose pour l'expression de
Sinon, merci dirac pour ton aide, je vais reprendre demain,relire tes remarques , revoir tout l'exercice au complet. Trier ce qui est juste de ce qui est faux, le rédiger de nouveau. Et enfin te proposer une solution qui je l'espère sera juste. Car actuellement je m'emmêle les pinceaux.
Merci beaucoup et à très bientôt 
Bon, histoire d'avancer le sujet je résume ce que nous avons établi:
1)
Donc en dérivant par rapport au temps dans le référentiel où les vecteurs
et
sont fixes:
2)
Donc en dérivant par rapport au temps dans le référentiel où les vecteurs
et
sont fixes:
3) Il nous reste à exprimer le vecteur vitesse d'entrainement tel que:
Et enfin nous souhaitons valider notre calcul par la comparaison du résultat avec la "formule":
Bonjour dirac et excuse moi pour le contre temps
Et enfin nous souhaitons valider notre calcul par la comparaison du résultat avec la "formule":
là, il faut que je bosse mon cours, car il y a un produit vectoriel qui me donnera certainement un vecteur hors du plan, et ça je ne comprends pas trop pourquoi??
Je n'ai absolument pas le temps d'aller plus loin maintenant, j'ai pris trop de retard sur d'autres matières.
Merci pour ton aide, je vais revenir c'est sûr, mais je dois avancer sur autre chose
Merci dirac
Pas de soucis ... c'est TON sujet 
Je crois que tu as compris l'essentiel: dans R' les vecteurs  ' et
' et  ' sont invariants
' sont invariants
Lorsque tu auras revu ton cours sur la représentation vectorielle de la rotation, le produit vectoriel ne te poseras aucun problème, j'en suis certain.
Juste, le dernier point "sympa" sera de noter que:
Donc
Tu vois donc que:
- dans le vecteur
est mobile, donc "on le dérive"
- la dérivation / temps du repère en rotation revient à une rotation de  /2 + une multiplication scalaire par la vitesse angulaire
/2 + une multiplication scalaire par la vitesse angulaire
Merci dirac, c'est super sympa, je vais relire mon cours et ensuite reprendre tout l'exercice.
à très bientôt
Bonjour,
Je reviens sur l'expression
Quelle est la différence entre ce vecteur : et celui-ci :
J'ai fais une recherche sur wikipédia, et le premier est un vecteur vitesse angulaire.
et le second est le vecteur vitesse appliqué au point O', ce qui revient presque au même.
Suis-je dans le vrai et y-a-t-il un rapport de entre les deux.
Merci mousse
Hello
Suis-je dans le vrai et y-a-t-il un rapport de

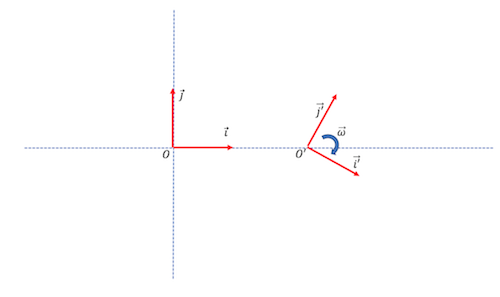
Un exemple peut être pour t'en convaincre? Dans le dessin ci dessous
O' a dans R' un mouvement rectiligne le long de Ox
Et R' tourne par rapport à R le long de l'axe O'z' (perpendiculaire au plan de l'écran)
C'est bon?
Hello Mousse,
Et pour compléter ma réponse d'hier soir (je n'avais plus en tête l'historique du sujet ...),
en imaginant que (O', i', j', k') est un cube dont O' est un sommet, tu peux je pense te représenter que le mouvement de ce cube dans l'espace est la composition de 2 mouvements:
- un mouvement rectiligne le long de la droite D
- un mouvement de rotation autour d'un axe passant par O' et perpendiculaire au plan
le premier peut être décrit par le mouvement de O'
le second par la rotation de R' (i',j' ici) dans R (i,j ici)
C'est plus clair?


