Inscription / Connexion Nouveau Sujet
Changement de base
Bonjour, j'ai du mal pour passer d'une base à une autre.
Par exemple: En cartésien, dS=dxdy et en polaire: dS=rdrd .
.
Je me dis que c'est parce que = r
mais bon c'est assez brumeux dans mon esprit.
Je pense savoir à quoi correspondent chaque vecteurs unitaire dans chaque base :
en cartésien: les 3 vecteurs unitaires correspondent à 3 axes "immobile" perpendiculaire entre eux, donc leurs quantités infinitésimales pour un volume correspond bien à dV=dxdydz.
en polaire: est dirigé vers le point M et
perpendiculaire à l'autre vecteur unitaire, "montre l'angle"et s'exprime que quand
est dérivée par rapport au temps.
en cylindrique: c'est similaire au polaire mais on rajoute pour la hauteur. Mais je ne vois pas comment faire pour calculer dV, dV=
 d
d d
d dz.
dz.
en sphérique: similaire au polaire mais on rajoute le vecteur unitaire , perpendiculaire aux autres vecteurs unitaires "pour montrer l'angle en 3D". Mais je ne vois pas comment calculer dV,
dV=r2sin drd
drd d
d
Aussi que signifie la longueur de l'élément d'arc dl ? Est-ce juste une distance infinitésimale dans une direction et sens donnée ?
dl2 = dx2 + dy2 + dz2 (cartésien) = dr 2 + r2d 2 + r2sin2
2 + r2sin2 d
d 2 (sphérique) = dr2 + r2 d
2 (sphérique) = dr2 + r2 d 2 + dz2 (cylindrique)
2 + dz2 (cylindrique)
Est-ce que vous pouvez m'éclaircir ? Merci d'avance
Bonjour
Selon moi, il faut partir du vecteur déplacement élémentaire dans les différentes bases. Avec les notations habituelles rappelées sur les schémas ci-dessous :
Il faut absolument savoir retrouver facilement ces expressions. Attention : certains auteurs permutent en sphériques les rôles de  et
et  .
.
Outre les expressions des normes des vecteurs déplacements élémentaires, on peut facilement retrouver les expressions des volumes élémentaires en effectuant le produit des trois composantes :
On peut aussi facilement retrouver les expressions de certaines aires élémentaires de surfaces élémentaires. Par exemple, surface élémentaire d'un cylindre de rayon R : il suffit d'imaginer r=R = constante et de faire le produit des deux autres déplacements :
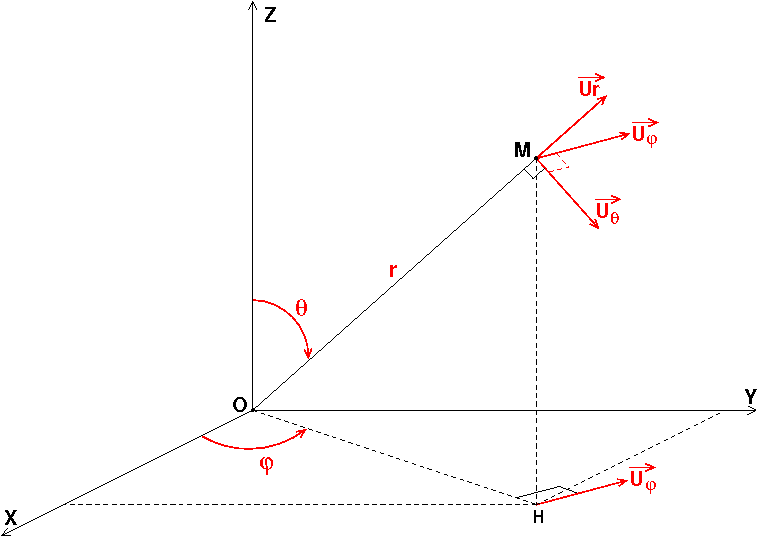
Autre exemple : aire élémentaire d'une portion élémentaire de surface sphérique de rayon R :
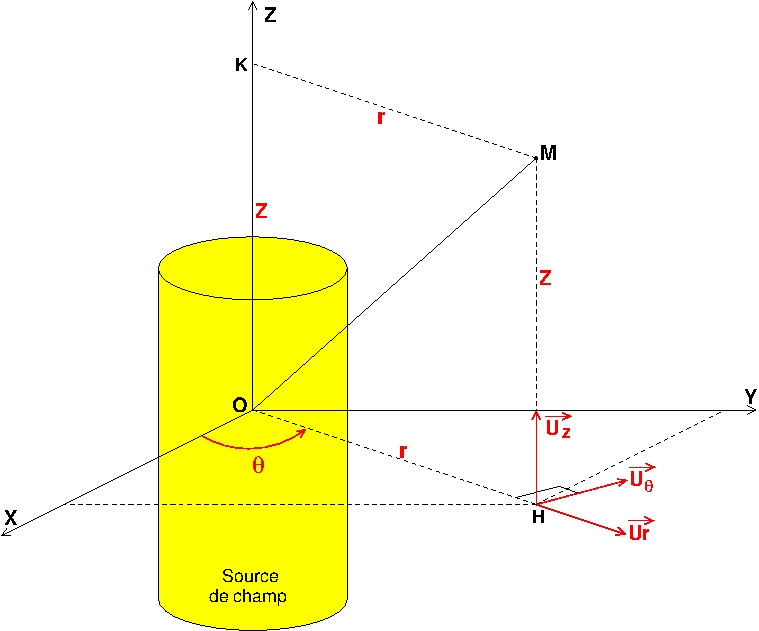
Erreur de manipulation de ma part : j'ai fourni deux fois le schéma correspondant aux coordonnées cylindriques (ne tient pas compte du cylindre en jaune). Voici le schéma correspondant aux coordonnées sphériques.
Tout d'abord merci pour ces explications claires.
Pour la base cylindrique je crois avoir compris:
sur ur et uz on fait un petit déplacement donc dr dz et pour u
 on dit que comme le déplacement est très petit, on peut le considérer comme un triangle rectangle. En regardant depuis l'origine et on s'intéresse au côté opposé donc côté opposé = sin * hypothénuse = sin ( d
on dit que comme le déplacement est très petit, on peut le considérer comme un triangle rectangle. En regardant depuis l'origine et on s'intéresse au côté opposé donc côté opposé = sin * hypothénuse = sin ( d  ) * r et comme d
) * r et comme d  est très petit on peut dire que sin
est très petit on peut dire que sin  =
=  donc vers u
donc vers u le déplacement élémentaire est r d
le déplacement élémentaire est r d .
.
Cependant, j'ai une mauvaise vision 3D pour la base sphérique, je n'arrive pas à voir le raisonnement vers u
 .
.
Ou c'est le même raisonnement que pour d mais cette fois-ci on s'intéresse par l'axe
mais cette fois-ci on s'intéresse par l'axe  donc c'est bien r sin(
donc c'est bien r sin( ) et pas d
) et pas d . Côté opposé = sin d
. Côté opposé = sin d x hyp(r sin
x hyp(r sin ) donc le résultar donne bien petit r sin
) donc le résultar donne bien petit r sin d
d
Tu imagines un déplacement élémentaire à r fixe et  fixe au cours duquel l'ange
fixe au cours duquel l'ange  varie de d
varie de d .
.
Le point M de mon dernier schéma se déplace sur un cercle d'axe (O,z) et de rayon MK où K est le projeté orthogonal de M sur l'axe (Oz).
Évidemment :
MK = HO=r.sin( )
)
Par définition du radian, le déplacement élémentaire dans ce cas particulier est :
Cette méthode peut être appliquer à toutes les composantes des vecteurs déplacements élémentaires.
Je pensais parce que le déplacement élémentaire vers l'axe  est r.d(sin
est r.d(sin ) et sin(x) de pi/2 à 3pi/2 = sin(x) de 3pi/2 à pi/2 mais comme on dit 0 à pi et non pi/2 à 3pi/2 ça me parait bizarre
) et sin(x) de pi/2 à 3pi/2 = sin(x) de 3pi/2 à pi/2 mais comme on dit 0 à pi et non pi/2 à 3pi/2 ça me parait bizarre
Je voulais dire que la valeur de sin(x) est symétrique par rapport qux ordonnées donc toute les valeurs de sin(x) de pi/2 à 3pi/2 correspondent à leurs symétriques sur 3pi/2 à 5pi/2
J'ai du mal à comprendre pourquoi [0,
 ] et non 2
] et non 2
Reprends mon schéma précédent et imagine sur une sphère de centre O et de rayon r=R un petit déplacement élémentaire
 de zéro à 2
de zéro à 2 rad. Tu dessines alors sur la sphère une couronne. Suppose maintenant que tu fasses varier
rad. Tu dessines alors sur la sphère une couronne. Suppose maintenant que tu fasses varier  de zéro à (
de zéro à ( /2)rad. Tu "balaies" ainsi la demie sphère telle que z>0. Si tu fais varier
/2)rad. Tu "balaies" ainsi la demie sphère telle que z>0. Si tu fais varier  de (
de ( /2)rad à
/2)rad à  rad, tu "balaies" alors la demie sphère correspondant à z<0. Tu vois bien que balayer la sphère entière revient à faire varier
rad, tu "balaies" alors la demie sphère correspondant à z<0. Tu vois bien que balayer la sphère entière revient à faire varier  entre zéro et
entre zéro et  rad.
rad.
Pour t'assurer que tu as bien compris mes divers messages, si tu as un peu de temps devant toi, tu peux t'entraîner à retrouver l'expression de l'aire d'une sphère de rayon R et l'expression du volume d'une boule de rayon R.

 [0,
[0,
