Inscription / Connexion Nouveau Sujet
Champs electro-magnétiques: étude d'un accélérateur de particule
Bonjour, je bloque sur un exercice de physique dont voici l'énoncé:
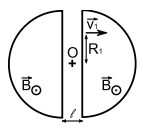
Le cyclotron est un accélérateur de particules, constitué de deux demi-cylindres métalliques D et D′ , appelés « dees », d'axe vertical commun (Oz ), placés dans le vide, et dans lesquels règne un champ magnétostatique uniforme et constant B
Les deux demi-cylindres sont séparés d'une distance l, sur laquelle les particules sont accélérées grâce à une différence de potentiel sinusoïdale u(t)=Um*cos(ωt). Une particule de masse m et de charge q > 0 est injectée dans le dispositif au voisinage de O, avec une vitesse v1 sur une trajectoire circulaire centrée en O de rayon R1
Le temps de passage d'un dee à l'autre est négligeable, et l'étude se fait dans le cadre de la mécanique newtonienne
J'ai fait la première question consistant à trouver la fréquence optimale pour l'accélération des particules, je trouve
Ensuite on appelle R1, R2, ... , Rn les rayons successfis des demi-cercles. Et il faut calculer, quelque soit n, Rn en fonction de R1, q, m, B, n, v1 et Um.
Mais je n'arrive pas à trouver comment procéder...
Merci d'avance pour toute indication 
Bonjour,
Le problème est dans le cadre de la mécanique classique (Newtonienne) avec un mouvement circulaire uniforme à l'intérieur des cylindres.
Tu as trouvé la bonne fréquence, qui est la fréquence de Larmor. Maintenant ton problème est de trouver le rayon de Larmor.
Le mouvement est circulaire uniforme dans un demi-cylindre, donc la force de Laplace exercée par le champ B compense exactement la force d'accélération centrifuge.
m r w^2 = qB*v;
w = pulsation de Larmor = 2*pi*qB/m et w (vitesse angulaire) est constante
et lien avec la vitesse w*r = v
=> r_1 = v_1 /w; et r_n = v_n /w.
Maintenant je te laisse trouver le lien entre les vitesses initiales sachant
que la particule gagne de l'énergie cinétique par le travail de la force électrique entre les deux cylindres séparés de la distance l.
Merci !
Ca n'était pas si difficile que ça en fait, j'obtiens
La suite ne me pose pas de difficultés, sauf un question question supplémentaire trouvée sur Internet. Je n'ai donc pas à la traiter, mais elle m'intrigue car je n'arrive pas à y répondre:
"On suppose que l'injection se fait en continue au centre de l'accélérateur. On constate cependant que les protons arrivent à la sortie par paquets séparés les uns des autres par le même intervalle de temps. Expliquer l'origine de ces paquets et calculer l'intervalle de temps séparant deux paquets de protons. "
Ce qui m'intéresse ici est l'origine des paquets. J'ai pensé à la répulsion électrique entre les protons lorsqu'ils sont sur des rayons proches, mais je ne pense pas que ça puisse expliquer correctement le phénomène...


