Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

champ uniforme

Posté par
moussolony 15-01-20 à 23:57

bonsoir

Énoncée :

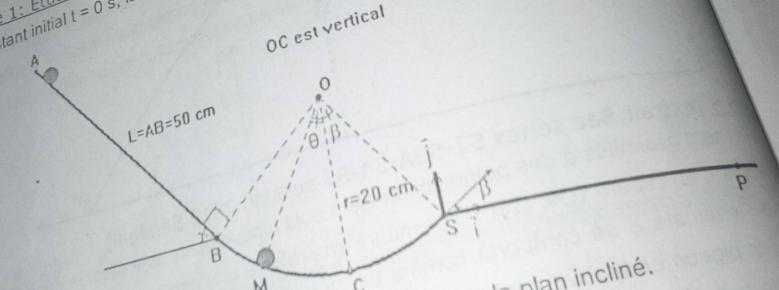
Une bille de masse m =30 g se déplace sans frottement sur un trajet ABS représente ci dessous. AB est un plan incliné de longueur AB= L=50 cm faisant un angle a =30° avec l horizontale et BC est un arc de cercle de centre O et de rayon r=20 cm.donnée : g=9,8 N/kg

Les parties 1,2,3 sont indépendant
Partie 1: étude du mouvement du solide sur le plan incliné
A l instant initial t=0 s , la bille est lâche sans vitesse au point A

1/déterminer l expression de l accélération de la bille sur le plan incliné
2/en déduis la nature du mouvement.
3/ déterminer l équation horaire de la bille sur le plan incliné (le point A étant choisi comme origine des espaces)
4/déterminer la date et la vitesse de la bille lors de son passage au point B.

Partie 2: étude du mouvement de la bille dans la glissière.
La bille aborde la partie circulaire BS avec une vitesse VB=2,20 m/s
La bille est repérée au point M par son abscisse angulaire O=MOC

1/ exprimer la vitesse de la bille en M en fonction de g,r,O,a et VB sachant que BOC=a
2/ exprimer l intensité de la réaction R de la bille en fonction de m,g,r,O,VB et a
3/indique le point où cette réaction est maximale. Justifie et calcule cette valeur.
4/ determine  la vitesse de la bille au point S sachant que B=COS=20°

Partie 3: mouvement de chute libre de la bille
La bille quitte a t=0, le plan au point s avec une vitesse Vs=2,26 m/s faisant un angle B avec l horizontale.
1/établis les équations horaires du mouvement de la bille dans le repéré (S,i,j)
2/ déterminer l équation cartésienne de la trajectoire de la bille .
3/ en déduis la nature du mouvement
4/ determine la flèche et l abscisse du point d impact P

champ uniforme

Posté par
moussolonyre : champ uniforme 16-01-20 à 00:07

Bonsoir
Partie 1
J ai répondu a ces questions sans une difficulté.mais la partie 2
J ai besoin d aider


Partie 2
Question 1
\frac{1}{2}*m*V^2M-\frac{1}{2}*m*V^2B=m*g*h
VM=√(2gh+V^2B))

Je n arrive pas trouver h en fonction de r,O,a

Posté par
diracre : champ uniforme 16-01-20 à 07:23

Hello

En considérant l'axe Oz vertical dirigé vers le bas:

z(B) = r.cos(a) \\ z(M) = r.cos(\theta)

h = z(M) - z(B) = r(cos(a) - cos(\theta))

Posté par
moussolonyre : champ uniforme 16-01-20 à 13:28

Bonjour
Pourriez m explique comment vous avez trouvé ces formules?

Posté par
diracre : champ uniforme 16-01-20 à 20:37

Bon, j'ai hésité à refaire un schéma ... et puis, je me suis dit qu'on allait y arriver sans

Appelons  Mx   tout axe horizontal orienté vers la droite
Appelons  Mz   tout axe horizontal orienté vers le bas


\widehat{ABx} = a

Donc \widehat{BOC} = \widehat{BOz} = a

Est ce qu'arrivé là on est bon?  Si oui on a fait le plus dur, si non, il va falloir que je fasse un schéma

Posté par
moussolonyre : champ uniforme 17-01-20 à 05:10

Bonjour
oui, un schéma

Posté par
diracre : champ uniforme 17-01-20 à 07:26

Hello

Citation :
oui, un schéma


(un petit mot d'encouragement n'est jamais de refus: "merci", "s'il te plaît", "m'aiderait bien", .... )

Bref, toute  affaire cessante, les schémas qui devraient t'aider à y voir plus clair

(attention ces schémas ne sont pas à l'échelle, en particulier l'angle a vaut bien plus que la valeur de l'énoncé, mais c'est justement pour plus de clarté)

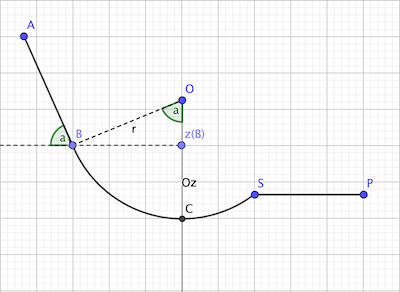
1er schéma l'angle a de l'énoncé (l'angle que fait AB par rapport à l'horizontale) est également l'angle que fait OB par rapport à la verticale: normal car l'énoncé indique que    \widehat{OBA} = \frac{\pi}{2}

Donc , z(B) étant la coordonnée de B sur l'axe Oz:   z(B) = r.cos(a)

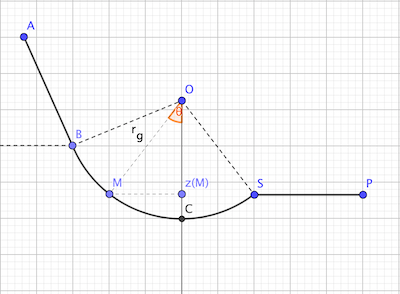
2eme schéma: la masse M repérée par l'angle

On a de la même manière  z(M) = r.cos()

Te voici remis en selle?

champ uniforme

champ uniforme

Posté par
moussolonyre : champ uniforme 18-01-20 à 15:26

J ai compris maintenant
Merci pour les schémas

Posté par
moussolonyre : champ uniforme 18-01-20 à 15:54

VM=√(2gr(cosO-cosa)+V^2B)

Question 2
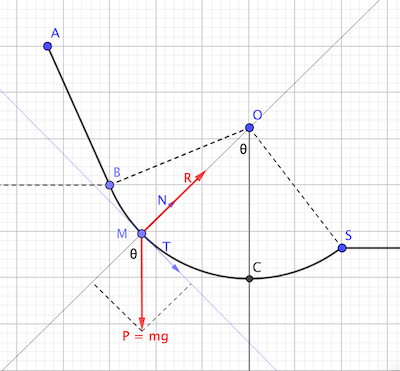
Appliquons le théorème du centre d inertie
P+R=m*a

Projection dans le repéré MO

-P+R=m*\frac{V^2M}{r}
-m*g*h+R=m*(V^2M)/r

R=m*(V^2M)/r+mg r(cosO-cosa)

R=m[(2gr(cosO-cosa)/r+gr(cosO-cosa)

R=mg[2(cosO-cosa)+r(cosO-cosa)
C est ça

Posté par
diracre : champ uniforme 19-01-20 à 08:03

Citation :
Projection dans le repéré MO

-P+R=m*\frac{V^2M}{r}
-m*g*h+R=m*(V^2M)/r




La projection du poids sur l'axe (MO) du repère de Frenet n'est pas "mgh"  mais plutôt -mgcos

Donc R = mgcos\theta + \frac{m}{r}(2gr(cos\theta - cosa)+v_B^2)

Et donc R = \frac{mv^2_B}{r} + mg(3cos\theta - 2cosa)

A toi?

Posté par
moussolonyre : champ uniforme 20-01-20 à 22:30

Bonsoir
S il plaît ,m aiderait avec un schéma

Posté par
diracre : champ uniforme 21-01-20 à 11:56

Il faudra te familiariser avec les projections de la rfd sur les axes d'un repère

Ici tu avais fait le choix judicieux d'un repère de Frenet attaché au mobile M:  (M, \vec{T}, \vec{N})

La RFD s'écrit:   \vec{R} + m\vec{g} = m\vec{a}

Donc en projetant sur l'axe tex](M, \vec{N})[/tex]

+R-mgcos\theta = ma_N = m\frac{v^2}{r}

Soit R = mgcos\theta +m\frac{v^2}{r}

Ce qui conduit à l'expression de R que je te fournissais dans mon précédent message

champ uniforme

Posté par
moussolonyre : champ uniforme 21-01-20 à 18:11

OK, j ai compris
Question 3
Je suis bloqué

Posté par
diracre : champ uniforme 21-01-20 à 18:50

Citation :
Je suis bloqué


Tu rigoles! j'ai passé en revue tes sujets/messages sur l'... tu sais le faire.  Allez un petit effort avant que nous t'aidions, 10 ... 9 ... 8 ...

Posté par
diracre : champ uniforme 22-01-20 à 04:58

... 3, 2, 1 ... 0

Donc dans la 3eme partie du mouvement, on munit le plan de la trajectoire du repère (S,\vec{i}\vec{j})

La seule force s'exerçant sur la masse est le poids

RFD:  m\vec{a} = m\vec{g}

En projection sur les axes:

\ddot{x} = 0 \\ \ddot{y} = -g

En intégrant et en utilisant les conditions initiale ( à t = 0 M est en S(0,0) avec la vitesse \vec{v}_S = v_S(cos\beta\vec{i} + sin\beta\vec{j})

x(t) = v_Scos\beta t \\ y(t) = -\frac{1}{2}gt^2 + v_Ssin\beta t

Equation cartésienne:  ( t = \frac{x}{v_Scos\beta} )

y(x) = -\frac{g}{2v_S^2}(1+tg^2\beta)x^2 + tg\beta x

3/ et 4/ ne doivent pas te poser de problème?

Posté par
moussolonyre : champ uniforme 23-01-20 à 16:43

Bonjour
non, je parlais plutôt de la partie 2
Voici la question 3
indiquer le point ou cette réaction est maximale .justifier ta réponse

Posté par
diracre : champ uniforme 23-01-20 à 21:12

Euh ... suis perplexe

Nous avions établi ensemble (ou presque)

R(\theta) = mgcos\theta +m\frac{v^2}{r}

Donc

R(\theta) = acos\theta + b

Avec a et b 2 constantes positives

Et     \theta \in [-30° , +20°]

Donc R() passe par un maximum pour = ???

Posté par
moussolonyre : champ uniforme 25-01-20 à 23:56

O=-3O°

Posté par
diracre : champ uniforme 26-01-20 à 09:13

Ah pas vraiment, peux tu aller rechercher dans ton cours les valeurs des maximas et minimas de la fonction cosinus?

Posté par
moussolonyre : champ uniforme 26-01-20 à 20:52

Bonsoir
-1 et 1

Posté par
diracre : champ uniforme 26-01-20 à 21:38

Parfait

Donc le max de cos(x) vaut 1 et le min vaut -1

Pour quelles valeurs de x?

Posté par
moussolonyre : champ uniforme 26-01-20 à 22:36

x=180°
x=0

Posté par
diracre : champ uniforme 27-01-20 à 05:40

Donc, puisque la fonction cos(x) passe par un maximum pour x = 0

La réaction qui s'exprime comme R() = a. + b avec a et b positifs, passe par un maximum pour = ?

Posté par
moussolonyre : champ uniforme 28-01-20 à 23:47

O=a+b

Posté par
diracre : champ uniforme 04-02-20 à 22:22

il y avait une coquille dans mon msg du 27/01

On a donc R() = a.cos +b

avec a et b 2 constantes positives (disons a = b = 1) et variant dans l'intervalle [-30°,+20°].

Pour quelle valeur de est ce que R() = cos+1 est maximale?  (pour t'aider cette valeur maximale vaut 2)

Donc?

Posté par
moussolonyre : champ uniforme 07-02-20 à 12:55

Bonjour
Cette valeur est
R(2)=cos2+1
R(2)=1,99 N

Posté par
diracre : champ uniforme 08-02-20 à 06:01



Bon, il va falloir se fendre d'un corrigé détaillé car tu t'égares à nouveau:

Le 19/01 à 8:03, nous avions établi:

R(\theta) = \frac{mv^2_B}{r} + mg(3cos\theta - 2cosa)

Soit R(\theta) =3mg.cos\theta + (\frac{mv^2_B}{r} - 2mgcosa) avec \theta \in [-30°, +20°]

Sur cet intervalle cos\theta passe par un maximum pour \theta = 0  où  cos\theta prend la valeur 1 (si cela n'est pas "évident" pour toi je t'engage sérieusement à revoir ton cours de trigonométrie)

Donc la réaction R atteint une valeur maximale en \theta = 0 avec:

R(0) =3mg + \frac{mv^2_B}{r} - 2mgcosa

ma calculette dort encore, je te laisse le soin d'effectuer le calcul numérique demandé.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !