Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

champ uniforme

Posté par
moussolony 09-01-20 à 23:13

Bonjour
Énoncé:

Dans tout l exercice, on suppose que le mouvement des protons a lieu dans le vide et on negligle leur poids par rapport aux autres forces .on considéré le dispositif de la figure 1
Des protons sont émis en C avec une vitesse quasiment nulle,puis accéléré entre les points C et D des plaques P1 et P2


1 /précise le signe de la tension UCD pour que les protons soient accélérés.
Justifie la réponse .
2. On posera pour la suite |UCD|=U
2/1 exprimer la vitesse VD d un proton en D en fonction de U, e,et MP
2/2 calculer VD
,3/après la traversée de la plaque P2 en D  les protons pénètrent en 0 entre deux plaques parallèles P3 et P4 de longueur l et distantes de d.la tension U' appliquée a ces plaques créé un champ électrostatique uniforme E .donnée : l=20 cm , et d=7 cm

3/1 montre que l énergie cinétique d un proton se conserve entre D et O.
3/2 .Établis dans le repéré (0,i.j), les équations horaires du mouvement d un proton dans les régions limitée par les plaques P3 et P4
3/3 vérifié que l équation de la trajectoire peut s écrire : y=\frac{-U'*x^2}{4*d*U}
3/4 déterminer la condition a laquelle doit satisfaire la tension U' .pour que les protons sortent du champ électrostatique E sans heurter la plaque P4
3/5 .determiner U' pour que les protons sortent du champ en passant par le point S de coordonnées {l,(-d/5)}
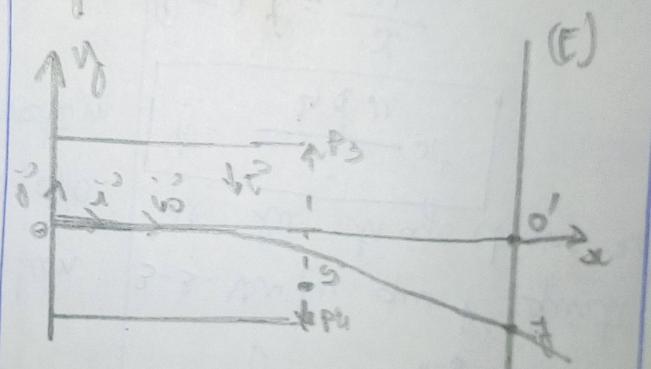
4/ a la sortie du champ électrostatique par le point S.les protons sont reçus en un point J, sur un écran plat et placé perpendiculaire a l axe OX
4/1.représente qualitativement la trajectoire d un proton entre les points O et J .
4/2 établis l expression littérale de la déviation O'J' du spot sur l écran (E)
4/3 .calcule la distance O'J'
On donne
L=20 cm, U=10^3 V, mp=1,67*10^-27 kg ; OI=l/2,e=1,6*10^-19 c.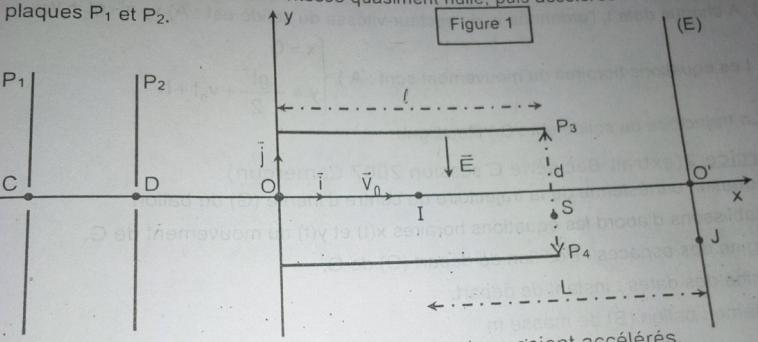

champ uniforme

***[edit modération] : recadrage image***

Posté par
moussolonyre : champ uniforme 09-01-20 à 23:34


Question 1
Le signe de UCD est positif, car les protons sont émis en C et ils sont accélérés entre C et D
On a
VC-VD>0

Question 2/1
Application du théorème de l énergie cinétique
EC(D)-EC(C)=W(Fe
1/2*m*V^2D=qU
VD=√(2*q*U)/mp)
VD=√(2*e*U/mp)
2*e*U=2*1000*1,6*10^-19
2*e*U=3,2*10^-19
VD=√(3,2*10^-6/1,67*10^-27)
VD=4,1*10^5 m/s

Question 3/1
Application de la conservation entre D et O
Em(D)=Em(O)
EP(D)=Ep+O)=0
EC(D)=EC(O)
Donc l énergie cinétique d un proton se conserve entre D et O .

Question 3/2
Système : les protons
Référentiel: terrestre supposé galiléen
Inventaires des forces
La force électrostatique
Application du théorème du centre d inertie
Fe=m*a
q*E=m*a
a=q*E/m
Projections dans le repère choisi
a t=0,OM{x0=0,yo=0 .  V{vox=VO, voy=0}
a t différent de 0
Application du théorème du centre d inertie
a=(q*E)/m=-q*E/m*j{ ax=0,ay=-qE/m}

OM{x(t)=vot, y(t)=-q*E/2*m t^2}

Question 3/3
t=x/VO
y=\frac{-q*E*x^2}{2*m*V^2O}
Mon problème a ce niveau, je n arrive pas a trouver l expression demandee

Posté par
odbugt1re : champ uniforme 10-01-20 à 00:58

Bonsoir,

Il te faut utiliser :
a) La relation entre le champ électrique et la tension entre les plaques P3 et P4
b) La relation que tu as trouvée à la question 2.1

Posté par
moussolonyre : champ uniforme 10-01-20 à 01:13

OK
y=(-q*E*x^2)/(2*mp*V^20) or E=U'/d
y=(-q*U'*x^2)/(2*MP*V^2O)
Et v^2O=V^2D=(2*q*U)/mp
y=(-q*U'*x^2)/(2*mp*d) * 1/(V^2O)


y=(-q*U'*x^2)/(2*mp*d)*mp / (2qU)

y=-(U'x^2)/(2*d*U)

Posté par
moussolonyre : champ uniforme 10-01-20 à 01:15

y=(-U'*x^2)/4*d*U

Posté par
moussolonyre : champ uniforme 10-01-20 à 01:17

J aimerais savoir si ma réponse 1et 2/1 sont exactes

Posté par
moussolonyre : champ uniforme 10-01-20 à 01:18

Question 3/4
Je suis bloqué

Posté par
odbugt1re : champ uniforme 10-01-20 à 10:31

Question 1:
La réponse est exacte. Ta justification, qui ne justifie rien, est une recopie de l'énoncé.

Question 2.1 :
La relation est exacte.
Je trouve un résultat numérique un peu différent, probablement à cause d'erreurs d'arrondis.

Question 3.3 :  Merci, à l'avenir, d'employer de vrais indices, de vrais exposants.
Je suis un peu las d'avoir à déchiffrer (par exemple) que :
2*MP*V^2O signifie pour toi 2* mP * (V0)²

Posté par
moussolonyre : champ uniforme 10-01-20 à 12:59

Question 1
Comment justifier ma réponse?

Posté par
moussolonyre : champ uniforme 10-01-20 à 13:00

Question 2/1
Quel résultat numérique, vous avez trouvé

Posté par
odbugt1re : champ uniforme 10-01-20 à 13:32

Citation :
Question 1
Comment justifier ma réponse?

J'attends une proposition de ta part pour en discuter.


Citation :
Question 2/1
Quel résultat numérique, vous avez trouvé

Je te retourne la question en t'invitant à revoir tes calculs en évitant de trop arrondir tes résultats intermédiaires.

Posté par
moussolonyre : champ uniforme 11-01-20 à 13:31

Question 1
Pour ma part, la chargée portée par les protons est positives .cela veut dire que la force électrostatique et le vecteur champ ont le même sens .d après l énoncé les protons sont accélérés entre C et D.d où le champ E est orienté de C vers D
On aura donc
VC-VD>0

Posté par
odbugt1re : champ uniforme 11-01-20 à 13:33

C'est très bien !cc

Posté par
moussolonyre : champ uniforme 11-01-20 à 13:49

Question 2/1
2*e*U=2*1000*1,6*10^-19
2*e,*U=3,2*10^-16

VD=(\frac{2*U*e}{mp})
VD=(3.2*10^-16))/1,67*10^-27))
VD=VD=4,4*10^5 m/s

Posté par
odbugt1re : champ uniforme 11-01-20 à 14:37

Oui, c'est aussi ce que j'ai trouvé.

Posté par
moussolonyre : champ uniforme 11-01-20 à 18:54

Question 3/4
Je ne sais pas quoi faire

Posté par
odbugt1re : champ uniforme 11-01-20 à 21:01

Question 3/4

Les protons sortent du champ électrostatique sans heurter la plaque P4 si pour x=l on a y -d/2

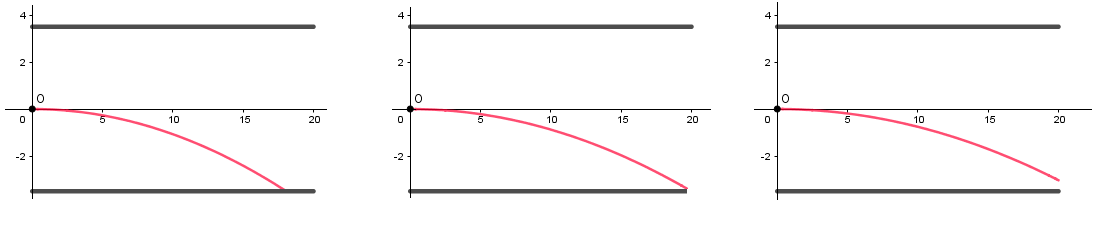
champ uniforme

Posté par
moussolonyre : champ uniforme 11-01-20 à 21:50

Question 3/5
Je suis bloqué encore

Posté par
odbugt1re : champ uniforme 11-01-20 à 23:14

1er cas :
U' est trop grand, les protons sont trop déviés et heurtent la plaque : y(l) < -d/2
2e cas :
Cas limite. y(l) = -d/2
3e cas : Les protons sortent du champ sans heurter la plaque : y(l) > -d/2

Il faut résoudre l'équation y(l) > -d/2, l'inconnue étant U'

Posté par
moussolonyre : champ uniforme 12-01-20 à 21:55

y(I)>-d/2
(U'*X^2I)/(4*U*d)+d/2>0

\frac{0,01U'}{280}+\frac{0.07}{2}>0
\frac{0,01U'}{280}>-0 ,035
0,01U'>-9,8

U'>-980

Posté par
odbugt1re : champ uniforme 12-01-20 à 23:32

Non
J'ignore ce qu'est pour toi X^2I

On a y(l) = -  \dfrac{U'~l^2}{4~U~d}
L'inéquation à résoudre est y(l) - d/2
donc :

-  \dfrac{U'~l^2}{4~U~d}  \geq - \dfrac{d}{2}

ce qui équivaut à :

U' \leq 2~U\left( \dfrac{d}{l} \right)^2

Posté par
moussolonyre : champ uniforme 15-01-20 à 22:12

Bonsoir

U'<2000*(0,07/0,2)^2
U'<2000*0,1225
U'<245

Posté par
moussolonyre : champ uniforme 15-01-20 à 22:14

Question 4/1

champ uniforme

Posté par
moussolonyre : champ uniforme 15-01-20 à 22:15

Question 4/2
Je n arrive pas établis l expression

Posté par
odbugt1re : champ uniforme 15-01-20 à 23:49

Question 3/4 :

Citation :
U'<245
Je ne vérifie plus les résultats qui n'ont pas d'unité.

Questions 3/5
Non faite ?

Question 4/1:
Ton schéma de très mauvaise qualité ne montre pas l'essentiel :
Quelle est la différence de la nature de la trajectoire des protons quand ils sont dans le champ puis hors du champ électrique ?

Question 4/2
Citation :
Je n arrive pas établis l expression
La réponse à la question 4/1 aide à résoudre la question 4/2

Posté par
odbugt1re : champ uniforme 15-01-20 à 23:59

Aide à la question 4.1 : Voir le schéma ci-dessous

champ uniforme

Posté par
moussolonyre : champ uniforme 16-01-20 à 00:12

Question 3/4
U<245 V

Posté par
moussolonyre : champ uniforme 16-01-20 à 00:17

Question 3/5
Avant de faire le calculer voici ma méthode
y(l)>(-d)/2

Posté par
moussolonyre : champ uniforme 16-01-20 à 00:18

C est plutôt
y(l)>(-d)/5

Posté par
moussolonyre : champ uniforme 16-01-20 à 00:24

Question 4/2
Je suis encore bloqué

Posté par
odbugt1re : champ uniforme 16-01-20 à 00:44

Question 3.4 :
Exact

Question 3.5 :
Non
Ce n'est pas une inéquation qu'il faut résoudre mais une équation .
Laquelle ?

Posté par
moussolonyre : champ uniforme 16-01-20 à 00:50

y(l)+(d)/5=0

Posté par
odbugt1re : champ uniforme 16-01-20 à 10:22

Oui, c'est bien cela.

Posté par
moussolonyre : champ uniforme 18-01-20 à 11:02

Bonjour
Question 3/5
y(I)+d/5=0
\frac{-U'l^2}{4*d*U}+\frac{d}{5}=0


U'=\frac{4*d^2*U}{5*l^2}

4*d^2*U=4*1000*(0,07)^2=19,6 V/m^2
5l^2=5*0,2*0,2=0,2 m^2

U'=(19,6)/0,2
U'=98 V

Posté par
odbugt1re : champ uniforme 18-01-20 à 20:42

Oui, c'est exact même si ton 19,6 V/m² est en réalité 19,6 V.m²

Posté par
moussolonyre : champ uniforme 19-01-20 à 01:13

Question 4/2
Tan a=(O'J)/IO'=(2ys)/l
IO'=d-l/2

(OJ')=(-q*U'*l)/4*d*U*(d-l/2)

C est ça

Posté par
odbugt1re : champ uniforme 19-01-20 à 11:08

Question 4.1
Non faite.
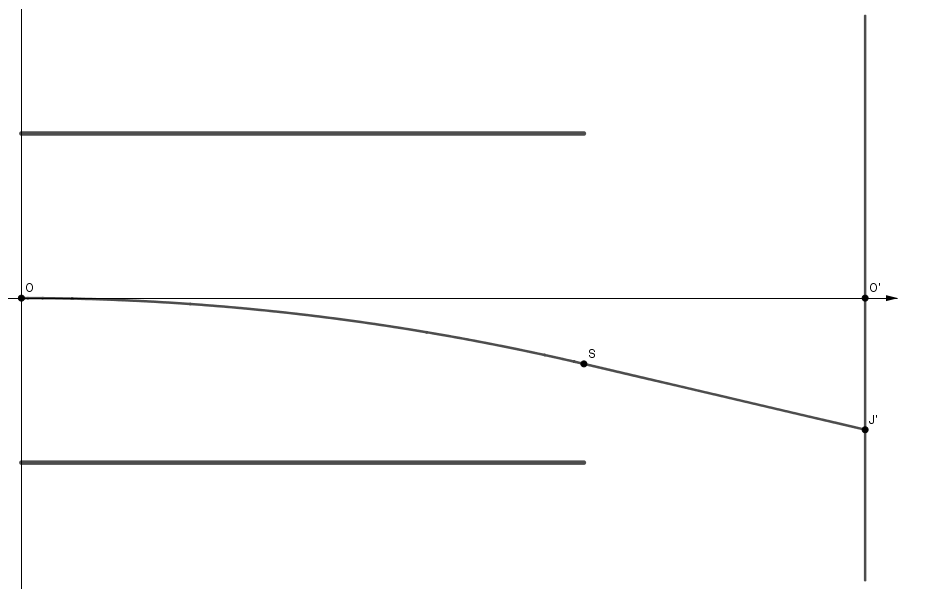
Il faut tenir compte du fait que la trajectoire des protons qui est parabolique entre les plaques, ne l'est plus en dehors, en expliquer la raison et faire la représentation demandée en conséquence.

Question 4.2 A l'aide (par exemple) du théorème de Thalès on démontre que :
O'J' = 2yS

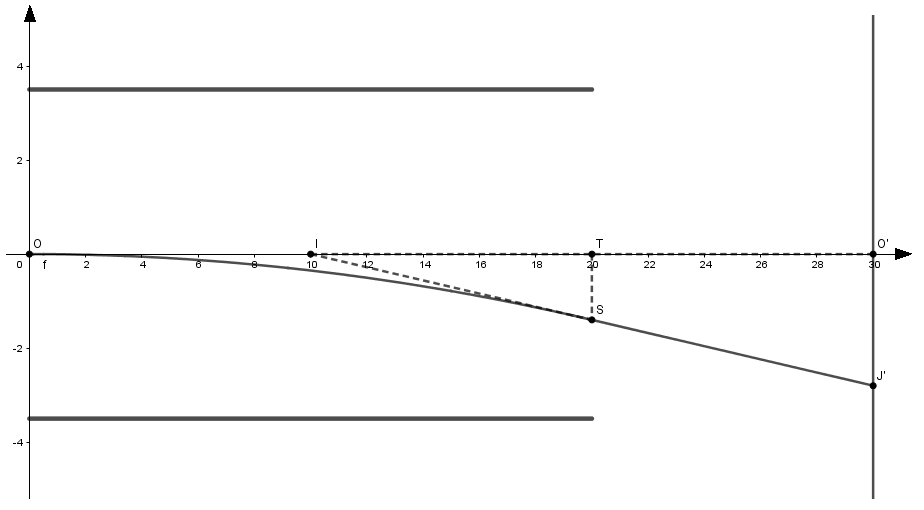
champ uniforme

Posté par
moussolonyre : champ uniforme 25-01-20 à 23:53

Question 4/2
Je n arrive pas a trouver l expression

Posté par
odbugt1re : champ uniforme 26-01-20 à 00:08

Dans mon dernier post :
Je t'ai indiqué la méthode, je t'ai fait la figure.
Alors, si malgré tout, tu as un problème tu pourrais me semble t'il poser des questions précises plutôt que le peu constructif  " Je n'arrive pas "

Posté par
moussolonyre : champ uniforme 26-01-20 à 11:33

OK,pourquoi .
O'J=2*ys

Posté par
moussolonyre : champ uniforme 26-01-20 à 11:40

Si O'J=2ys
On aura donc

O'J=2*\frac{-U'x^2}{2d}
O'J=\frac{-U'x^2}{d}

Posté par
odbugt1re : champ uniforme 26-01-20 à 14:25

Ton post du 26-01-20 à 11:33
La réponse à ta question se trouve dans mon post du 19-01-20 à 11:08
Bien entendu, cela suppose que tu connaisses le théorème de Thalès.

Ton post du 26-01-20 à 11:40
Ton résultat n'est pas homogène donc il est faux.
En effet O'J est une longueur alors que - U' x² / d n'en est pas une


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !