Inscription / Connexion Nouveau Sujet
Champ magnétique sur l'axe d'un cylindre
Bonjour
énoncé
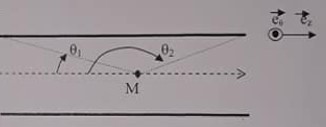
Un cylindre de rayon R de longueur l est le siège d'une densité surfacique sur sa face latérale Js=jsetheta
Déterminer l'induction magnétique créée en un point M de l'axe du cylindre.
donc j'utilise la loi du biot et savart après avoir trouvé la direction du B (suivant -z, sym(M,er,etheta)
dB=μ0 *R^2*Js/4 *dl*PM*sin( ) t.q
) t.q  est l'angle entre PM et l'axe Z
est l'angle entre PM et l'axe Z
mais j'ai du mal de trouver le dl puisque le courant est suivant e
si quelqu'un peut me guider un peu, ça serait super
merci d'avance
Bonjour
La méthode consiste à partir de l'expression de B sur l'axe d'une bobine plate de N spires vue sous l'angle theta d'un point M de l'axe.
On découpe ensuite le solénoïde en tranches élémentaire de hauteur dz et on fait la somme des vecteur champ élémentaires...
Il s'agit de démontrer la formule que tu viens d'écrire en utilisant la méthode que je t'ai indiquée précédemment.
Tu trouves facilement la démonstration sur le net. Poses des questions précises sur ce que tu ne comprends pas bien.
Oui, j'ai déjà démontré cette formule, mais l'exercice demande l'induction au niveau d'un cylindre et pas un solénoïde?
C'est la même démonstration. Il suffit juste pour terminer d'établir la relation simple entre js et n.I.
Considère un solénoïde constitué d'un enroulement jointif d'un fil conducteur de très faible diamètre sur un cylindre de rayon R très grand devant le diamètre du fil. J'appelle ”n” le nombre de spires par unité de longueur. Cet enroulement jointif est équivalent à une distribution surfacique de courant. Soit un petite surface rectangulaire élémentaire de cette nappe de courant de largeur dz, mesurer suivant l'axe du solénoïde et de longueur dl mesurée suivant . Dans l'expression de la loi de Biot et Savart, cet élément de courant peut être caractérisé par le vecteur
.
A raison de n fils parcourus par le courant d'intensité I par unité de longueur, le ruban élémentaire de largeur dz contient n.dz fils conducteurs et est ainsi parcouru par le courant élémentaire n.I.dz. Dans l'expression de la loi de Biot et Savart, on peut remplacer par
. Par identification :

 Bs ndz ?
Bs ndz ?


