Inscription / Connexion Nouveau Sujet
Champ magnétique et force linéaire
Bonjour, je bloque sur un exercice portant sur le magnétisme, pouvez vous m'aider svp ?
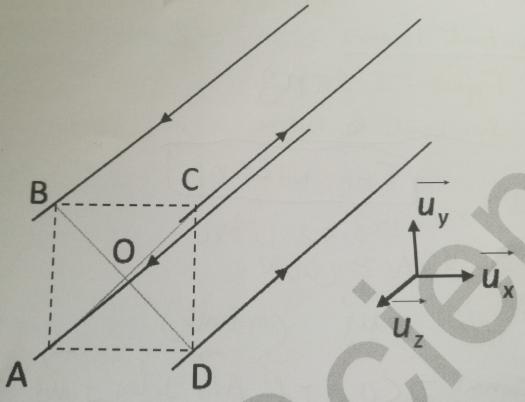
Quatre fils conducteurs supposés infinis sont disposés sur les arêtes d'un carré ABCD de 5 cm de côté; Chacun d'eux est parcouru par un courant dont le sens est donné sur le schéma ci-dessous et d'intensité I=15A
On donne =4pi.10^-7T.m/A
Quelles sont les composantes selon x, y et z de la force agissant sur 1m du fil A, exprimées en mN ?
Une réponse exacte :
A(0, 0,45, -1,35°
B(-1,35, 0,45, 0)
C (1,35 , -0,45, 0)
D(-1,35 -0,45 0)
E(1,35 0 -0,45)
Alors je sais que le fil A intéragit avec les 3 autres fils
et puisque ce sont des fils infinis, il faut utiliser la formule de la force linéaire :
I1 et I2 l'intensité du fil 1 et 2
mais après je ne sais pas comment faire ??
Merci de m'aider 
Bonjour,
Il n'y a plus qu'à additionner les trois forces, mais attention addition vectorielle, donc un dessin avant de faire le calcul est une bonne idée, dessin en vue de dessus dans le plan Oxy.
Bonjour, oui merci
Donc si je poursuis cette démarche, il faut que je prenne également en compte les axes je suppose par exemple
je fais seulement un calcul de Fb (Force entre le fil B et A) selon Uy ? (puisque AB est selon Uy )
pareil pour Fc et Fd qui seront selon Uz (pour Fc) et Ux (pour Fd ) ?
ou je fais le calcul selon les 3 axes pour chaque fil puis j'additionne selon la composante ? (Fb+Fc+Fd selon Uy selon Ux et selon Uz par exemple ?)
je ne sais pas si c'eest clair
Merci
C'est bien clair, mais
- attention aux signes (en fonction du sens des courants)
- pour Fc, la direction CA n'est pas dans la direction de uz, de nouveau faites un dessin.
Donc j'ai pris en compte le sens des courants et donc du signe de chaque vecteur, je ne sais pas si cest bon
J'ai donc : (vFb= vecteur Fb) (a= coté du carré= 5cm) (vUxyz=vecteur U des 3 axes)
Pour Fc je ne suis pas sûr, cela me semble bizarre selon (Uy+Ux)
Est ce exact svp ? 
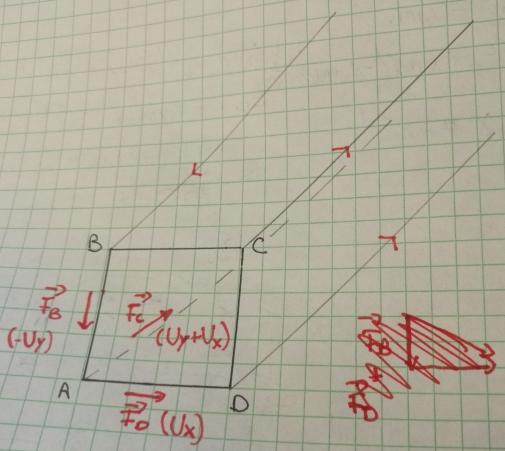
Cela me parait partir dans la bonne direction.
Deux remarques :
- deux fils parallèles parcourus par des courants de même sens s'attirent, j'ai l'impression que vous avez fait l'inverse.
- pour Fc, il y a en effet un problème n'est pas unitaire, il faut donc diviser par sa norme (mais c'est bien la bonne direction).
merci
Mais quand vous parlez des fils qui s'attirent si les courants sont dans le même sens, vous parlez des signes des expressions je suppose ?
si c'est la cas, alors cela donne ceci je pense ( car avant je n'avais pas pris en compte le sens du courant du fil A) :
Fb>0
Fc<0 (car Ic et Ia sont de sens opposés)
de même pour Fd <0
je ne sais pas si cest ceci que vous insinuez ?
car avant, concernant les signes des 3 expressions, je faisais en fonction de si le vecteur BA était opposé au vecteur Uy par exemple (de même pour AD et AC )
Un vecteur n'a pas de signe, c'est pour cela que je parlais d'attraction.
Fb est de même sens que uy
Fd est de sens opposé à ux
Fc a le même sens que
Donc, en effet, sauf erreur de ma part ! En notant
,
et
ce qui donne la même chose que vous si vos IA et IB ... sont algébriques
Je ne comprends pas trop comment avez vous fait pour trouver le sens de Fb Fc Fd ? a partir de quelle principe ?
(dailleurs dans ce que vous avez ecrit, n'est ce pas plutot Fd=-kUx ?)
et pourquoi pour Fc c'est quand même k alors que Fc ne représente pas un coté du carré et donc ce n'est pas "a" mais racine(2)a ?
et d'où sort le divisé par 2 dans Fc ?
désole mais je suis un peu perdu 
Mes excuses pour la faute de frappe : c'est bien x pour Fd.
Pour trouver le signe, on peut partir de zéro, ce que vous avez peut-être fait : on cherche le sens de B (tire-bouchon, bonhomme d'Ampère ...), puis on cherche le sens de la force (trie-bouchon, règle des trois doigts ...). Vous devriez, sauf erreur de ma part ! la même chose.
Pour éviter ceci, je suis parti du fait que "les fils s'attirent si les courants vont dans le même sens", IA et IB étant de même sens, on sait donc que A est attiré par B.
Le 1/2 de Fc est en fait , le premier terme venant de la distance, le deuxième de la norme de (ux+uy).
Merci pour toutes vos explications
j'ai compris a peu pres l'essentiel
donc il me reste plus qu'a additionner ces 3 composantes ? Ux avec Ux , Uy avec Uy, et Uz avec Uz (ce qui donne Uz=0 je suppose puisque aucun des trois FB Fc Fd n'a de Uz ?)
ps: question toute bête, mais pour moi la norme d'un vecteur c'est bien alors pourquoi 1/racine(2)


