Inscription / Connexion Nouveau Sujet
Champ magnétique et aimant
Bonjour,
Pouvez vous me dire si ce que je dis est bon,
Un aimant (pole + et -) peut il attirer de ces deux poles une tôle en fer ? J'ai un petit doute mais pour moi je pense que oui si la tole n'est pas aimantée.
Enfin, je n'arrive pas bien à comprendre la représentation coulombienne. Pourquoi sur la photo du bas, H est en sens inverse dans l'aimant ?
Merci !
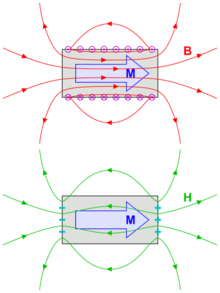
Bonjour
Un aimant (pole + et -) peut il attirer de ces deux pôles une tôle en fer ?
La réponse est oui. On montre que la force exercée sur un échantillon de matière non aimantée placée dans un champ magnétique est proportionnelle au gradient de
je n'arrive pas bien à comprendre la représentation coulombienne.
Je n'avais plus entendu parler de masses magnétiques depuis des décennies. Cette notion qui conduit à traiter l'aimant droit comme un condensateur plan induit parfois des idées fausses... Dans le cas d'un condensateur plan, écarter les deux armatures permet de séparer des charges plus d'une part, des charges moins d'autre part. Si tu coupes en deux un aimant droit, tu n'obtiens pas un pôle nord d'un côté (une masse magnétique nord) et un pôle sud de l'autre (une masse magnétique sud) mais bien deux nouveaux aimants plus courts, chacun doté d'un pôle nord et d'un pôle sud.
Cela dit : les lignes de champ pour
Imagine une ligne de champ pour
Cela n'est possible que pour un vecteur
Merci beaucoup,
Elle est d'autant plus intense que le champ magnétique est inhomogène ; elle est donc plus intense au voisinages des deux pôles de l'aimant.
Comment peut on montrer cela ?
Normalement dans un condensateur c'est le champ électrique qui va des charges + aux charges - mais ici comme on a une aimantation, on parle de H (qui va aussi du + et -).
Au fait, je ne comprends pas pourquoi dans le dessin du haut, on a B et pas H (car H est crée par le courant NI) Est ce parce que on considère la reponse du matériau donc H + l'aimantation ?
De même dans le second cas, une aimantation ne crée pas normalement un champ magnétique B ? (si pas de courant)
Comment peut on montrer cela ?
On part de l'expression de la force de Laplace exercée sur un dipôle magnétique (petite spire circulaire parcourue par un courant) de moment magnétique
On s'intéresse ensuite à un volume élémentaire de matière aimantée qui possède un moment magnétique élémentaire
Le paragraphe 10.2 du même document apporte des précisions sur les différents vecteurs intervenant dans l'étude d'un barreau uniformément aimanté. De plus, l'ensemble du document est intéressant et précis dans ses notations.
D'accord, merci pour les explications.
Normalement dans un condensateur c'est le champ électrique qui va des charges + aux charges - mais ici comme on a une aimantation, on parle de H (qui va aussi du + et -).
Au fait, je ne comprends pas pourquoi dans le dessin du haut, on a B et pas H (car H est crée par le courant NI) Est ce parce que on considère la reponse du matériau donc H + l'aimantation ?
De même dans le second cas, une aimantation ne crée pas normalement un champ magnétique B ? (si pas de courant)
Du coup pour ces questions ?
Merci !
Il se trouve que la notion de masse magnétique fictives facilite la détermination de H alors que l'introduction de courant fictifs (les courants liés) facilite l'étude de B. Dans l'aimant et autour de l'aimant, le vecteur B se détermine comme si on était dans le vide en présence de courants fictifs ayant pour densité volumique :
et pour densité surfacique :
La démonstration est faite §10.1.3 du document que je t'ai fourni précédemment. Pour un barreau cylindrique uniformément aimanté comme ici, le rotationnel est le vecteur nul en tout point. En revanche, la densité surfacique n'est pas nulle : on est ramené à étudier le champ magnétique dans le vide créé par un solénoïde.
Concernant H : dans le vide autour de l'aimant :
A l'intérieur de l'aimant :
Cela explique le sens du vecteur H.
Merci !
Donc dans le premier cas, M étant considéré uniforme partout, on a donc que des courants surfaciques et donc on considère cela comme un solénoide donc B.
Dans le cas 2, on considère un réel aimant avec une aimantation et on a des charges de part et d'autre (les pôles ?). Et donc, en considérant H, on a bien ces lignes de champs.
M étant considéré uniforme partout
partout... en tout point de l'aimant mais M=0 à l'extérieur de l'aimant.
Les deux théorie conduisent au même résultats, c'est uniquement la méthode de calcul qui change.
Première méthode : on fait intervenir les courants fictifs (courants liés) qui permettent de déterminer B comme si on était dans le vide.On déduit ensuite H de la connaissance de B et de M.
Deuxième méthode (de moins en moins employée, quasi abandonnée dans l'enseignement supérieur) : on fait intervenir des charges magnétiques fictives qui permettent de déterminer H. On déduit ensuite B de la connaissance de H et de M.
Heureusement, les deux méthodes conduisent au même résultat. C'est juste pour plus de clarté que les schémas que tu as reproduits, tirés je pense de wikipédia, ne superposent pas les lignes de champ pour H et pour B en privilégiant B dans un cas et H dans l'autre.


