Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

champ magnétique bobine plate

Posté par
ferality 14-03-21 à 23:18

Bonjour,

J'ai un problème de niveau L2 physique que je n'arrive pas à résoudre, surtout la question 3 me pose problème. Voici l'énoncé :

On considère une bobine plate circulaire, d?épaisseur négligeable et comprenant N spires. On note O son centre, R son rayon et Oz l?axe normal aux spires. Cette bobine est parcourue par un courant d?intensité I constante. Le sens positif du courant est le sens trigonométrique défini par +\vec{u_z}.

1. En considérant les symétries, déterminer la direction du champ magnétique produit par la bobine au point O, \vec{B_b}(O)

- >J'ai fait cette question je trouve que le champ est orienté selon \vec{u_z}

2. Calculer \vec{B_b}(O) à l?aide de la loi de Biot et Savart.

-> J'ai fait cette question je trouve \vec{B_b}(O)=\dfrac{N\mu_0 I}{2R}\vec{u_z}

Ce qui est étrange c'est que cette ressource :
dit que c'est "R" et pas "2R"...

3.Une boussole peut être représentée par un moment magnétique (de norme constante, parallèle à l?aiguille et orienté de son pôle sud vers son pôle nord. On la plonge dans un champ magnétique uniforme \vec{B}.

Rappeler l?expression de l?énergie potentielle d?interaction entre l?aiguille et le champ magnétique. En déduire l?orientation de l?aiguille par rapport au champ \vec{B} quand elle est dans une configuration d?équilibre stable.

-> Ici je prend le champ \vec{B}(M)=\vec{B_b}(O).sin^3\alpha et calcule \dfrac{dEp}{d\alpha}=-M.B(0).3sin^2\alpha.cos\alpha=0 afin d'avoir un équilibre, puis \dfrac{d^2Ep}{d\alpha^2}=-M.B(0).6sin\alpha.cos^2\alpha - 3sin^3\alpha=0 ... je ne vois pas comment trouver un alpha tel que cette expression soit positive (pour avoir un point d'équilibre qui soit stable et non instable)

Je sais qu'à la fin je dois trouver que la position de stabilité est que le moment magnétique est orienté dans le même sens que le champ magnétique (donc l'angle alpha entre les deux est nul, alpha=0) mais je ne vois pas comment arriver à cette conclusion mathématiquement avec les calculs.

4. Soient O un point au voisinage de la surface terrestre, et (Ox) l?axe vertical ascendant en ce point. On place au point O une boussole dont l?aiguille est libre de tourner dans le plan horizontal x = 0 (l?aiguille est équilibrée pour qu?elle reste horizontale). On note \vec{u_y} l?orientation sud-nord de l?aiguille quand elle n?est soumise qu?au champ magnétique terrestre. On dispose la bobine étudiée plus haut dans le plan (Oxy) de telle sorte que son centre est le point O. Le sens positif du courant dans la bobine est le sens trigonométrique défini par \vec{u_z}.

Un  courant  d?intensité I non-nulle  circule  dans  la  bobine.  À  l?équilibre,  le  moment magnétique  de  l?aiguille  fait  avec  le  vecteur \vec{u_y} un  angle ?,  orienté  dans  le  sens trigonométrique  défini  par \vec{u_x}.  Exprimer  la  norme B_t de  la  composante  horizontale  du champ magnétique terrestre en fonction de ?, N, I, R et ?0. (On supposera que l?aiguille est  suffisamment  petite  pour  que  l?expression  du  champ  créé  par  la  bobine  en O reste valable à l?échelle de toute l?aiguille.)

-> Ici je pense que selon la même ressource :

Il faut poser tan\alpha = \dfrac{B_b(O)}{B_t(O)} et donc B_t(O) = \dfrac{\mu_0 N I}{2 R tan\alpha} est la réponse ?


Je serai très reconnaissant si vous pouvez m'aider, je bloque depuis un moment :[

***Raccourcis url ajoutés***

Posté par
vanoisere : champ magnétique bobine plate 14-03-21 à 23:54

Bonsoir
Le champ magnétique créé au centre d'une bobine plate est bien donnée par ton expression, celle faisant intervenir "2R" et non "R".
Pour 3 : tu te compliques la vie. Il s'agit de partir de l'expression de l'énergie potentielle d'un dipôle magnétique de moment \vec M dans un champ magnétique uniforme de vecteur \vec B. Le cube d'un sinus intervient dans un tout autre contexte.
La question 4 étudie la boussole des tangentes... Essaie de faire un schéma très clair des vecteur champ en présence, schéma que tu peux scanner et poster ici.

Posté par
feralityre : champ magnétique bobine plate 15-03-21 à 00:38

D'accord me voilà rassuré pour l'expression du champ.

Pour 3 : d'accord donc si je fais ça j'obtiens : Ep =-\vec{M}\cdot\vec{B} =-M.B.\cos\alpha puis \dfrac{dEp}{d\alpha}=M.B.\sin\alpha et \dfrac{d^2Ep}{d\alpha^2}=M.B.\cos\alpha donc \dfrac{d^2Ep}{d\alpha^2}>0 \iff M.B.\cos\alpha>0 \iff -\pi/2 < \alpha < \pi/2 je n'aboutis pas au résultat "que je veux" qui est d'avoir l'angle alpha égal à 0 ou égal à Pi.

J'ai fait le schéma (en considérant que le champ terrestre est selon u_y car c'est ce qui devrait être le cas si l'aiguille est en équilibre stable) que j'ai joint au message. Je ne vois pas en quoi ma réponse est erronée je continue de penser que tan\alpha = \dfrac{B_b(O)}{B_t(O)} est correct, je dois rater quelque chose.

J'avais aussi tenté un autre raisonnement qui était de dire que la somme des moments créés par les champs était nulle car on avait un équilibre : \Gamma_b + \Gamma_t = \vec{M}\wedge\vec{B_b}(O) + \vec{M}\wedge\vec{B_t}(O) = \vec{0} et donc M.B_b(O).sin(\pi/2 - \alpha) = M.B_t(O).sin(\alpha).  Puis sin(\pi/2 - \alpha) = cos(\alpha) et donc B_t(O)=\dfrac{B_b(O)}{tan\alpha}

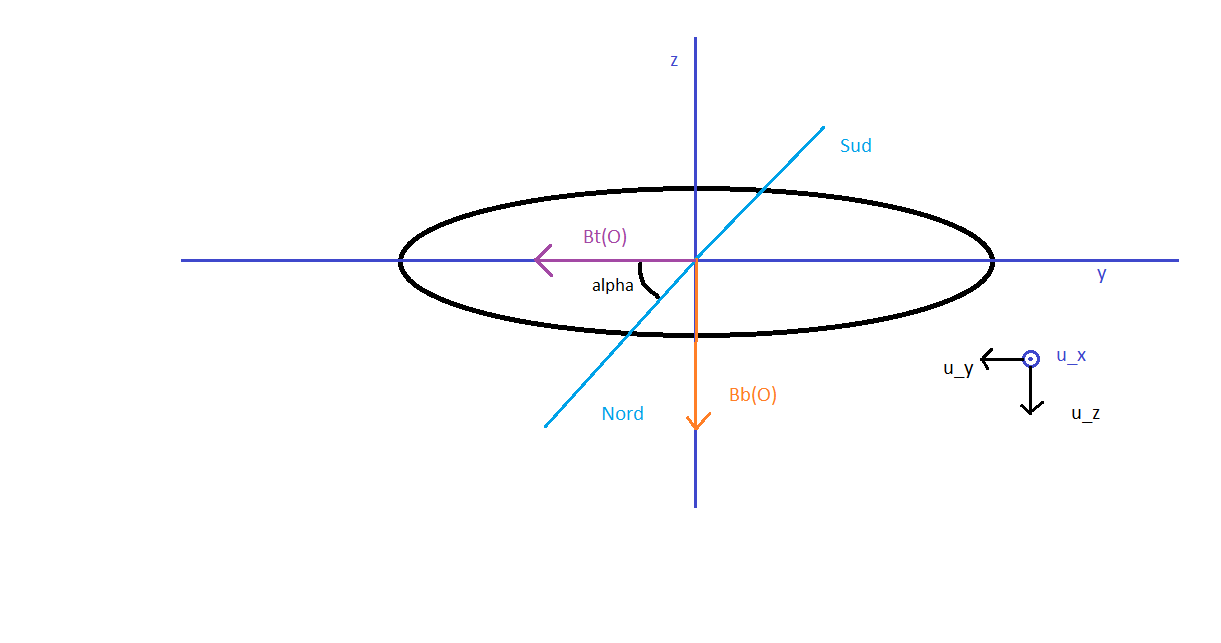
champ magnétique bobine plate

Posté par
feralityre : champ magnétique bobine plate 15-03-21 à 00:38

Bonsoir

Posté par
vanoisere : champ magnétique bobine plate 15-03-21 à 10:15

Pas tout à fait : l'aiguille de boussole est lestée pour compenser l'action de la composante verticale du champ magnétique terrestre.  Cela permet une comparaison des normes de la composante horizontale du champ terrestre et du champ créé par la bobine sous réserve que le champ créé par la bobine soit lui-même horizontal. Cela nécessite donc de placer la bobine dans un plan vertical. Pour que les calculs soit simples, le vecteur champ créé par la bobine doit être perpendiculaire à la composante horizontale du champ terrestre.
Tu dois refaire ton schéma en tenant compte de ces remarques.
Pour 3 : d'accord avec ton expression de Ep.
Équilibre stable pour un minimum de Ep donc un maximum du cosinus donc =0
Equilibre instable pour un maximum de Ep donc un minimum du cosinus donc : = rad (tout cela modulo 2 bien sûr).

Posté par
feralityre : champ magnétique bobine plate 15-03-21 à 14:00

Je ne suis pas sûr de bien comprendre... on a défini que le champ magnétique terrestre était selon \vec{u_y} (c'est pour ça que la boussole est alignée à cet endroit à la base, car elle est à l'équilibre vis à vis du champ magnétique terrestre, \alpha=0)

On sait aussi que le champ généré par la bobine est selon \vec{u_z}... donc Bt est selon \vec{u_y} et Bb selon \vec{u_z}. Désolé mais c'est tout ce que j'arrive à comprendre pour le moment

J'ai refait le schéma par dessus le schéma donné dans le problème qui est peut-être mieux que le mien :

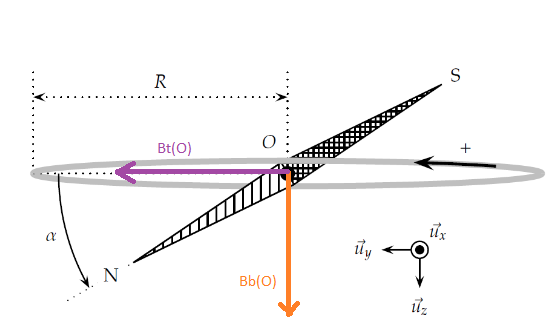
champ magnétique bobine plate

Posté par
vanoisere : champ magnétique bobine plate 15-03-21 à 15:47

Relis bien l'énoncé tel que tu l'as recopié : l'axe vertical est ici l'axe (Ox). La bobine plate appartient au plan vertical du méridien local. L'axe (Oy) est ainsi horizontal et orienté vers le nord. En absence de courant traversant la bobine, le pole nord de l'aiguille aimantée indique le nord magnétique, l'aiguille est orientée selon l'axe (Oy).
En présence d'un courant continu traversant la bobine (je n'ai pas dessiné le circuit d'alimentation de celle-ci) apparait un champ magnétique supplémentaire de vecteur \vec B horizontal, orienté suivant (O,Z) donc vers l'est.
L'aiguille aimantée tourne alors dans le plan horizontal (cela est bien précisé dans l'énoncé) d'un angle "a" de façon à indiquer la direction du vecteur somme (\vec B_t +\vec B)

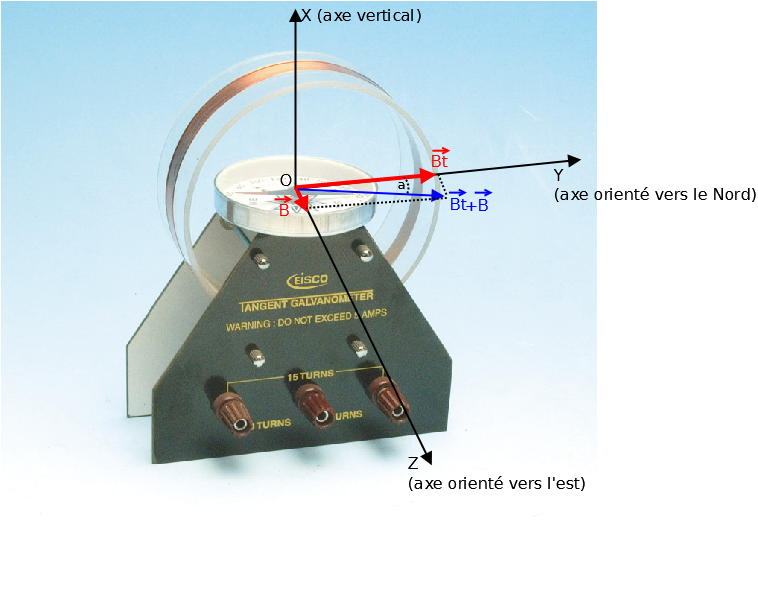
champ magnétique bobine plate

Posté par
feralityre : champ magnétique bobine plate 15-03-21 à 18:31

Oui j'ai l'impression qu'on dit exactement la même chose ! Je suis 100% d'accord avec ce que vous dites. Peut-être je me suis mal exprimé.
Mais donc même sur votre schéma on voit que tan(\alpha)=\dfrac{Bt}{B} ... donc je ne vois pas en quoi ce n'est pas la bonne approche

Posté par
feralityre : champ magnétique bobine plate 15-03-21 à 18:32

tan(\alpha)=\dfrac{B}{Bt} pardon

Posté par
vanoisere : champ magnétique bobine plate 15-03-21 à 18:46

D'accord avec ta dernière réponse.  Ton schéma précédent est effectivement une vue correcte d'une vue de dessus du dispositif.

Posté par
feralityre : champ magnétique bobine plate 15-03-21 à 19:20

D'accord donc la réponse à la question "Exprimer  la  norme B_t de  la  composante  horizontale  du champ magnétique terrestre en fonction de \alpha, N, I, R et µ0" est bien B_t = \dfrac{\mu_0 N I}{2 R tan\alpha}\vec{u_y} ?

Posté par
vanoisere : champ magnétique bobine plate 15-03-21 à 20:00

Oui !

Posté par
feralityre : champ magnétique bobine plate 15-03-21 à 20:15

Super merci beaucoup vanoise


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !