Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Champ et potentiel dans un gaz chargé

Posté par
kamikaz 25-10-21 à 03:50

Bonjour

La région de l'espace telle que |x| ≤ a porte une densité volumique de charge ρ . Elle est limité par deux plans x=a et x=-a

1) Calculer le champ électrostatique en tout point de l'espace.

2) Si on désigne par V0, le potentiel en O, que vaut le potentiel V en un point quelconque de l'espace.

3) Représenter la variation du champ et du potentiel en fonction de a.

Pourriez vous m'aider à faire un schéma s'il vous plaît

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 25-10-21 à 13:12

Bonjour
Il s'agit tout simplement d'une plaque uniformément chargée en volume d'épaisseur 2a  de longueur et de largeur infinies. L'origine du repère est le centre O de la plaque et l'axe Ox est perpendiculaire à la plaque.  Pour l'application du théorème de Gauss, utilise les indications de l'autre message.

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 02-11-21 à 08:50

ok, d'après le théorème de Gauss on a : \text{div} \vec{E}=\dfrac{\rho}{\epsilon _0}

Ce ne serait pas plutôt la longueur qui est infinie et la largeur 2a ?

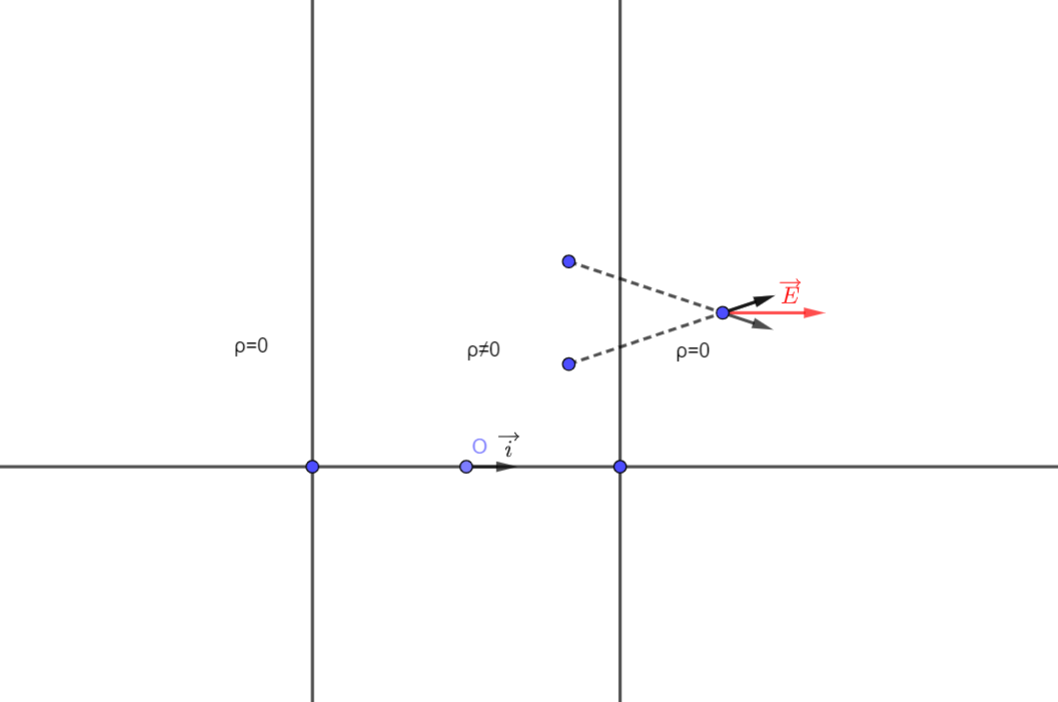
Champ et potentiel dans un gaz chargé

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 02-11-21 à 21:07

Je ne pense pas avoir commis d'erreur. Si tu préfères :
Les dimensions de la plaque suivant (Oy) et suivant (Oz) sont infinies. L'épaisseur, mesurée suivant (Ox), vaut 2a.
Tu peux effectivement montrer qu'en tout point de l'espace :
\vec E=E_{(x)}\cdot \vec{i}
Tu peux aussi montrer  que pour un couple de points M et M' tels que xM=-xM' :
\vec{E_M}=-\vec{E_{M'}}
Cela devrait t'aider à trouver une surface fermée permettant l'application du théorème de Gauss pour obtenir E(x).

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 03-11-21 à 06:36

Citation :
Tu peux aussi montrer  que pour un couple de points M et M' tels que xM=-xM' :
\vec{E_M}=-\vec{E_{M'}}


J'ai pas compris..

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 03-11-21 à 14:28

Toujours raisonner sur les plan de symétrie...
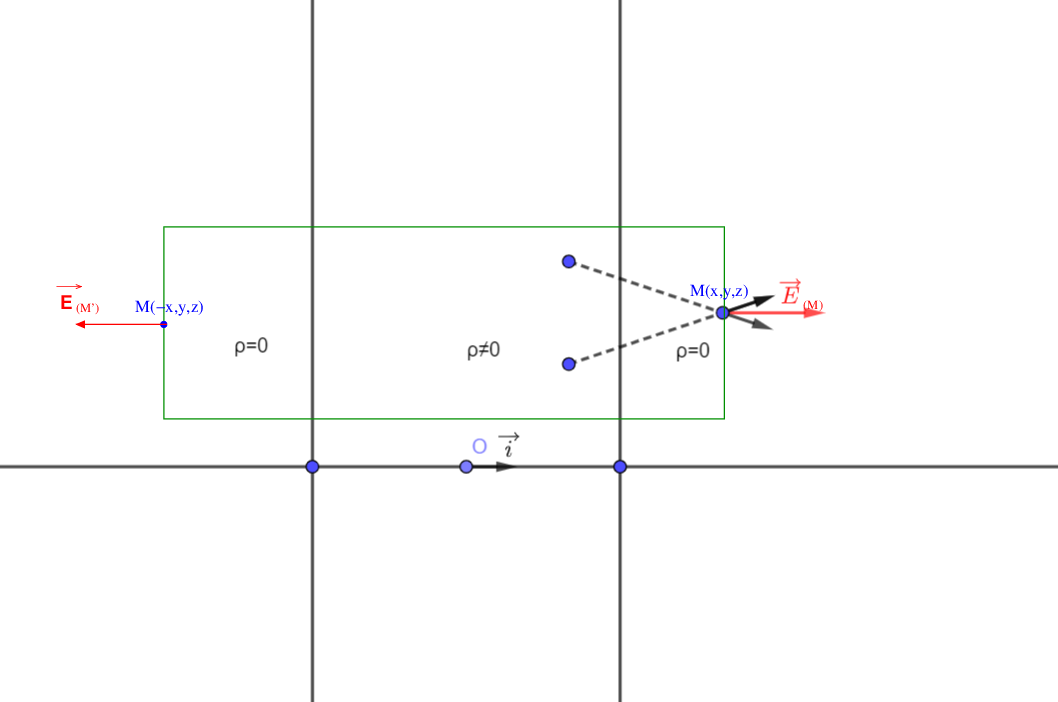
L'expression locale du théorème de Gauss faisant intervenir la divergence est sans intérêt pratique ici. Il faut faire intervenir le théorème de Gauss sous sa forme intégrée. Pour t'aider un peu, j'ai représenté en vert dans le plan de figure, la trace d'une surface de Gauss fermée possible : un cylindre dont les bases sont deux disques  d'aire S, centrés respectivement en M et en M'.

Champ et potentiel dans un gaz chargé

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 03-11-21 à 15:52

D'accord.

Citation :
Il faut faire intervenir le théorème de Gauss sous sa forme intégrée


\int \int _{\sum} \vec{E}.d \vec{S} ~\text{dv} = \int \int \int_v \dfrac{\rho}{\epsilon _0} \text{dv}

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 03-11-21 à 15:54

\int \int _{\sum} \vec{E}.d \vec{S} = \int \int \int_v \dfrac{\rho}{\epsilon _0} \text{dv}

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 03-11-21 à 16:04

Le flux du vecteur champ à travers la surface fermée est égal à la charge intérieure divisée par o.
Tu as donc trois flux à exprimer :
* celui à travers le disque d'aire S centré en M : il va faire intervenir E(x) ;
* celui à travers le disque d'aire S centré en M' : il fait intervenir aussi E(x) ;
*celui à travers la surface latérale du cylindre ; son expression est particulièrement simple...
Quand à la charge intérieure : tu vas être amené à distinguer deux cas :
1° : xa ;
2° : x>a.

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 03-11-21 à 18:32

*Flux à travers le disque d'aire S centré en M :

\phi _M = \int \int \vec{E} .d \vec{S} = \dfrac{1}{\epsilon _0}\int \int \int _v \rho dv

*Flux à travers le disque d'aire S' centré en M' :

\phi _M' =- \int \int \vec{E} .d \vec{S} =- \dfrac{1}{\epsilon _0}\int \int \int _v \rho dv

* Flux à travers la surface latérale  s du cylindre :

\phi = \int _s d \phi = \int _s \vec{A} . \vec{n} ds

\vec{A} : Le vecteur champ défini au point O

\vec{n} : La normale au plan de la surface latérale du cylindre.

* Charge intérieure

1er cas : x \le a

\sum Q_{int} = \dfrac{4\pi}{3} x^3 \rho

2e cas : x > 0

\sum Q_{int} = \dfrac{4\pi}{3} a^3 \rho

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 03-11-21 à 19:01

Il te faut vraiment revoir un cours sérieux et complet sur l'application du théorème de Gauss à la détermination du vecteur champ.Je vais t'aider dans le cas de la figure, soit pour x>a ; je te laisserai traiter l'autre cas ensuite...
*Flux à travers le disque d'aire S centré en M :
Le vecteur champ est constant en tout point du disque et perpendiculaire à la surface ; de plus le vecteur champ est orienté vers l'extérieur du volume délimité ; donc :
ΦM =E(x).S
*Flux à travers le disque d'aire S' centré en M' :
Par rapport à la situation précédente, le vecteur champ est devenu son opposé mais le vecteur surface est aussi devenu son opposé. Le flux, produit scalaire de ces deux vecteur est le même :
ΦM' =E(x).S
* Flux à travers la surface latérale  s du cylindre :
En tout point de cette surface lattérale, le vecteur champ, colinéaire au vecteur unitaire , est perpendiculaire à la surface. Le flux à travers la surface latérale est donc nul.
Φ=0
Le flux total à travers la surface fermée est ainsi :
Φt=2E(x).S
Pour x>a, la charge intérieure est celle contenu dans le cylindre de base d'aire S et de hauteur 2a :
Qint = .S.2a
Je te laisse en déduire l'expression de E(x) et traiter le cas xa.

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 03-11-21 à 23:13

Pourquoi la hauteur vaut 2a.

Comme le flux du vecteur champ électrostatique sortant d'une surface fermée est égal à la somme de la charge à l'intérieur de cette surface fermée divisée par  o.

On a : \phi _{\text{total}}=2E_{(x)}S et Q_{\text{intérieur}}=\rho S 2a

Donc \phi _{\text{total}}=\dfra{Q_{\text{intérieur}}}{\epsilon _0}

2E_{(x)}=\dfrac{\rho S 2a}{\epsilon _0}

E_{(x)}= \dfrac{\rho a}{\epsilon _0}

* Pour x \le a :

*Flux à travers le disque d'aire S centré en M :
Le vecteur champ est constant en tout point du disque et perpendiculaire à la surface ; de plus le vecteur champ est orienté vers l'extérieur du volume délimité et les vecteurs E et i sont opposés.; donc :
ΦM =-E(x).S

*Flux à travers le disque d'aire S' centré en M' :
les vecteurs E et i sont opposés.. Le flux, produit scalaire de ces deux vecteur est donc :
ΦM' =-E(x).S
* Flux à travers la surface latérale  s du cylindre :
En tout point de cette surface lattérale, le vecteur champ, colinéaire au vecteur unitaire , est perpendiculaire à la surface. Le flux à travers la surface latérale est donc nul.
Φ=0
Le flux total à travers la surface fermée est ainsi :
Φt=-2E(x).S
Pour x>a, la charge intérieure est celle contenu dans le cylindre de base d'aire S et de hauteur 2a :
Qint = .S.2a

Il vient donc : E_{(x)}=-\dfrac{\rho a}{\epsilon_0}

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 04-11-21 à 12:33

Citation :
\\ 2E_{(x)}=\dfrac{\rho S 2a}{\epsilon _0} \\ E_{(x)}= \dfrac{\rho a}{\epsilon _0}

Étourderie sûrement en utilisant l'éditeur d'équations Tex :

\\ 2S.E_{(x)}=\dfrac{\rho S 2a}{\epsilon _0} \\ \\ E_{(x)}= \dfrac{\rho a}{\epsilon _0} \\
Sinon, pour xa, les charges intérieures  sont les charges contenues dans le cylindre de hauteur 2x car le volume délimité par la surface de Gauss est entièrement dans la zone contenant une densité volumique de charge non nulle.
Qint = .S.2x

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 04-11-21 à 14:37

Ok,l'expression de E(x) que je trouve pour x ≤ a est bonne ?

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 04-11-21 à 14:58

Non : tu n'as pas tenu compte de mon dernier message ! E(x) dépend de la valeur de x si x est compris entre -a et +a...

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 04-11-21 à 19:08

Pour x>a  comment faites-vous pour savoir que le vecteur champ est constant en tout point du disque ou pas ? Comment çà se passe lorsque  -a < x ≤ a et comment représenter le vecteur E ?

Je trouve : E_{x} = \dfrac{\rho x}{\epsilon _0} mais en utilisant
div \vec{E}_{x} = \dfrac{dE_{x}}{dx}= \dfrac{\rho }{\epsilon_0} \Rightarrow E_{x} =\dfrac{\rho x}{\epsilon_0} sur l'intervalle [-a ; a] , E(x) est dérivable je ne sais pas si je peux expliquer comme çà mathématiquement

Mais j'ai pas compris pourquoi quand x est supérieur  à a on a le même a multiplié par rhô dans l'expression de E..

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 04-11-21 à 19:08

Pour x>a  comment faites-vous pour savoir que le vecteur champ est constant en tout point du disque ou pas ? Comment çà se passe lorsque  -a < x ≤ a et comment représenter le vecteur E ?

Je trouve : E_{x} = \dfrac{\rho x}{\epsilon _0} mais en utilisant
div \vec{E}_{x} = \dfrac{dE_{x}}{dx}= \dfrac{\rho }{\epsilon_0} \Rightarrow E_{x} =\dfrac{\rho x}{\epsilon_0} sur l'intervalle [-a ; a] , E(x) est dérivable je ne sais pas si je peux expliquer comme çà mathématiquement

Mais j'ai pas compris pourquoi quand x est supérieur  à a on a le même a multiplié par rhô dans l'expression de E..

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 04-11-21 à 19:25

Compte tenu de la logique déjà utilisée dans l'autre cas, pour xa :
2E(x).S=2.S.x/o
E(x)=.x/o
A titre de vérification, tu peux effectivement vérifier l'expression locale du théorème de Gauss :
x>a le point M appartient à une portion d'espace où =0.Il est donc logique d'obtenir une divergence du vecteur champ nulle.
Pour xa : est une constante positive. L'expression de la divergence déduite de l'expression du vecteur champ est correcte...

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 04-11-21 à 20:25

Ok, mais est ce qu'on ne devrait pas traiter le cas x < -a aussi ?

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 04-11-21 à 20:48

Oui, même si cela a été abordé en parlant des symétries et en appliquant le théorème de Gauss. Reprends la figure :

\overrightarrow{E_{(M')}}=-\overrightarrow{E_{(M)}}

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 04-11-21 à 20:57

Ok donc pour x < -a E_{(x)}=-\dfrac{\rho a}{\epsilon_0}

2) Comment calculer V pour un point quelconque ?

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 04-11-21 à 21:07

On a \dfrac{dV(x)}{dx}= -E(x) \Rightarrow V(x)= -\int E(x) dx

Est ce que calculer le potentiel V en un point quelconque de l'espace implique qu'on doit déterminer l'expression de V pour chacun des cas qu'on vient d'étudier pour E ?

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 04-11-21 à 21:19

Oui à ta dernière question.
La source du champ étant d'extension infinie, pas question de poser V=0  à l'infini.  On peut poser arbitrairement V=0 en x=0. Ce choix est arbitraire car seules les variations de potentiel ont un sens physique.
Tu as donc intérêt à étudier d'abord la situation où x est compris entre -a et a.
Pour les autres cas : ne pas oublier que V est fonction continue de x.

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 04-11-21 à 21:59

*Pour -a< x < a E_{x} = \dfrac{\rho x}{\epsilon _0} \Rightarrow V(x) = -\dfrac{\rho x²}{2\epsilon _0}

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 04-11-21 à 22:03

Oui  !

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 04-11-21 à 22:26

çà coince pour les deux..

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 04-11-21 à 22:53

Pour x < a E_{(x)}= \dfrac{\rho a}{\epsilon _0} \Rightarrow V(x) = - \dfrac{\rho a x}{\epsilon _0} \\

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 04-11-21 à 23:05

Tu oublies la constante d'intégration.
Pour x>a :

V=\dfrac{-\rho.a.x}{\varepsilon_{o}}+K_{1}

Pour trouver la constante d'intégration K1, on écrit la condition de continuité du potentiel en x=a.

Étude analogue ensuite pour x<-a.

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 05-11-21 à 06:12

Ok, mais pourriez vous faire un exemple pour le premier s'il vous plaît

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 06-11-21 à 19:42

Pour x > a V(x) = \dfrac{\rho a} \left(-x+ \dfrac{a}{2} \right)+V_0 ?

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 06-11-21 à 19:44

Oups

Pour x > a V(x) = \dfrac{\rho a}{\epsilon_0} \left(-x+ \dfrac{a}{2} \right)+V_0 ?

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 06-11-21 à 19:52

OK ; On peux convenir de poser V=0 si x=0

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 06-11-21 à 20:18

Donc on a : pour x > a V(x) = \dfrac{-\rho.a.x}{\varepsilon_{o}}+V_{0} = \dfrac{\rho a}{\epsilon_0} \left(-x+ \dfrac{a}{2} \right)+V_0 \\

Posté par
vanoisere : Champ et potentiel dans un gaz chargé 06-11-21 à 21:31

Tu peux poser Vo=0 puisque le potentiel est toujours défini à une constante près  : seules les variations de potentiel ont un sens physique. Ton résultat est correct.

Posté par
kamikazre : Champ et potentiel dans un gaz chargé 06-11-21 à 21:49

ok mais comment trouver l'expression de V si x < -a ?

Et comment représenter la variation du champ et du potentiel en fonction de a ?


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !