Niveau licence

Champ électrostatique dans une sphère

Posté par
oeufmimosa 09-10-23 à 17:34

Bonjour,

Je suis en première année en médecine. Je coince sur un exercice d'électromagnétisme.

Dans cet exercice, le potentiel électrique est considéré nul à l'infini.

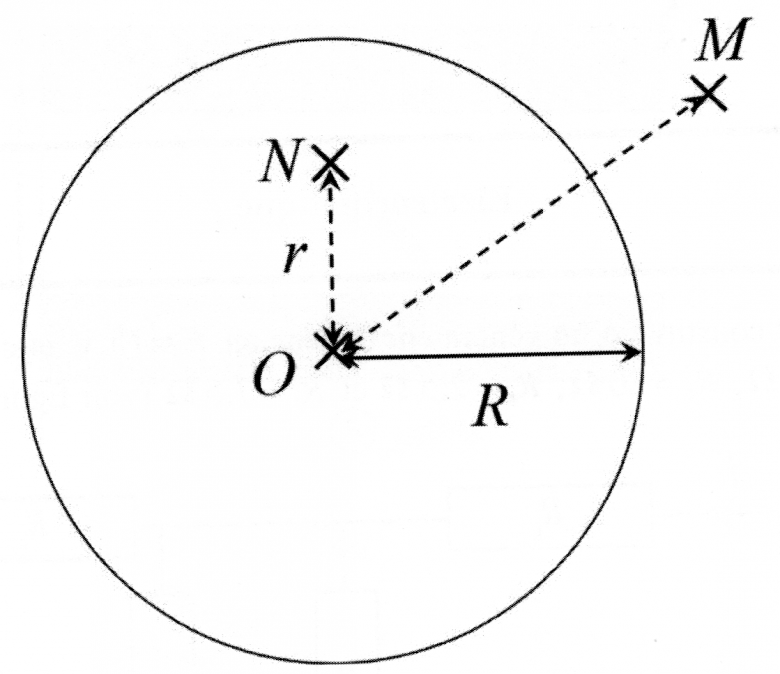
Une sphère pleine de centre O et de rayon R chargée uniformément en volume porte une densité de charge $\rho >0$ . On note $Q>0$ sa charge totale et $\vec{E}(N)$ le champ électrostatique crée à l'intérieur de la sphère en un point N situé à une distance $r<R$ du centre O. Le schéma est ci-dessous.

Première question, exprimer la densité de charge en fonction de Q. Pas de problème ici, je donne la réponse sans justifier le calcul qui est assez simple :
$\rho =\dfrac{3}{4}\dfrac{Q}{\pi R^3}$

Deuxième question, est-il vrai ou faux que $\vec{E}(N)$ décroit en $\dfrac{1}{r^2}$ ? Justifier la réponse.

Je crois comprendre que le théorème de Gauss s'applique ici, en calculant le champ au point N du schéma.
Je nomme $\vec{u_r}$ le vecteur unitaire tel que $\vec{ON}=r\vec{u_r}$ . Puisque la sphère est uniformément chargée, le champ ne dépend ni de $\theta$ ni de $\phi$ .

$\int \int \vec{E}(N) dS = \dfrac{Q}{\epsilon_0}$

Donc
$\vec{E}(N) \times 4\pi r^2 = \dfrac{4}{3} \dfrac{\rho r}{\epsilon_0}$
d'où
$\vec{E}(N)= \dfrac{\rho r}{3 \epsilon_0}$

Donc je trouve que le champ croit en r et non pas décroit en $\dfrac{1}{r^2}$
Je retrouve ce que j'ai vu en cours, c'est bon ici.

Troisième question :
On note V(N) le potentiel électrique créé à l'intérieur de la sphère en un point N à une distance 0<r<R.
On admet que le potentiel électrique V(M) à l'extérieur de la sphère
est :
$V(M)=\dfrac{\rho R^3}{3 \epsilon_0 r}$

Montrer que V(N)<0.

C'est ici que ça coince. La densité de charge est positive, pourquoi le potentiel serait-il négatif ?

Qui pourrait m'orienter ? Merci par avance.

Champ électrostatique dans une sphère

Posté par re : Champ électrostatique dans une sphère 09-10-23 à 18:49

Bonsoir
Pas sûr que la notion de gradient soit à ton programme mais tu as sans doute vu que, pour une source de champ à symétrie sphérique comme ici :
E=-dV/dr
ce qui revient à dire que V est une primitive par rapport à r de (-E). Une primitive n'est définie qu'à une constante près. Pour obtenir cette constante, tu considères la continuité de V en r=R. L'expression en r=R que tu vas obtenir doit être égale à celle valide à l'extérieur de la sphère en r=R.

Posté par re : Champ électrostatique dans une sphère 09-10-23 à 19:36

Bonsoir,

Je n'ai pas vu le gradient en cours. Je suis donc allé chercher sur Google. Effectivement, je ne comprends pas cette notion...
En revanche je confirme avoir vu le principe de symétrie sphérique, mais j'ai beau voir et revoir mon cours, je ne trouve pas cette équation différentielle : E=-dV/dr. Je crois que le mieux est d'aller voir mon prof mais je n'ai pas cours avec lui d'ici la semaine prochaine.

La dérivée du potentiel par rapport au rayon ne me parle pas, je ne vois pas ce qu'elle implique. Néanmoins cela me donne une piste à chercher sur internet. Cela devrait m'aider.

Merci pour cette réponse.

Posté par re : Champ électrostatique dans une sphère 09-10-23 à 19:41

r étant la variable, une primitive de (-r) vaut -½r². Rien de trop difficile mais je ne vois pas comment un professeur peut poser cet exercice sans avoir expliqué la formule E=-dV/dr et sans avoir expliqué que V est fonction continue des coordonnées d'espace...

Posté par re : Champ électrostatique dans une sphère 15-10-23 à 19:28

Bonsoir,

Pour la question 3, le potentiel ne peut être négatif partout dans la sphère si on prend l'expression suggérée à l'extérieur de celle-ci. Le potentiel est une fonction continue dans la configuration suggérée car il vérifie l'équation de Poisson, et que rho est continue par morceau. Et on voit que pour r=R, il est strictement positif en utilisant l'expression de l'énoncé, donc il existe un voisinage de R tel que le potentiel est strictement positif.

Mais cela n'exclut pas qu'il existe des valeurs de r telles que V est négatif (je n'ai pas effectué le calcul).

Bon courage

Posté par re : Champ électrostatique dans une sphère 15-10-23 à 20:05

Effectivement oeufmimosa semble avoir lâché l'exercice. Je le termine car cela peut intéresser d'autres étudiants et il y a une erreur d'énoncé à corriger.

Pour r<R :

$\dfrac{dV}{dr}=-E=-\dfrac{\rho.r}{3\varepsilon_{o}}$

Par intégration :

$V=-\dfrac{\rho.r^{2}}{6\varepsilon_{o}}+K$

avec K : constante d'intégration que l'on déduit de la relation de continuité du potentiel en r=R.

$-\dfrac{\rho.R^{2}}{6\varepsilon_{o}}+K=\dfrac{\rho.R^{2}}{3\varepsilon_{o}}\quad soit\quad K=\dfrac{3\rho.R^{2}}{6\varepsilon_{o}}$

D'où l'expression du potentiel électrostatique à l'intérieur de la boule :

$V=\dfrac{\rho}{6\varepsilon_{o}}\cdot\left(3R^{2}-r^{2}\right)$

V est fonction monotone décroissante de r mais est constamment positif, autant à l'intérieur de la boule qu'à l'extérieur. Comme l'avait intuitivement remarqué oeufmimosa, une source d'extension finie constituée de charges positives ne peut en aucun point créer un potentiel négatif quand on convient de considérer comme nul le potentiel infiniment loin de cette source.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Champ électrostatique dans une sphère

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique