Niveau licence

champ électrique d'une onde dans un milieu

Posté par
Jorg2 24-10-16 à 11:53

Bonjour!

Me revoilà avec mes questions.
J'aimerais avoir votre avis sur ma résolution d'un exercice d'optique:

Une onde monochromatique de 550 nm incide sur une surface eau/air avec un angle de 60°. Sa polarisation est linéaire formant un angle de 45° du plan d'incidence et son amplitude Eo=2 N/C

a) obtenir le vecteur d'onde transmise:
Pour moi, il n'y a pas d'onde transmise car l'angle critique est de 48,8° environ, est on a ici un angle de 60°. Je peux dire que k=0.

b) Ecrire l'expression du champ électrique de l'onde réfléchie exprimée en composants parallèles et perpendiculaires.
$r\perp =\frac{E_{r}}{E_{i}} \Rightarrow E_{r} = r\perp * E_{i} \\ r\perp = -\frac{sen(\theta _{i}-\theta _{t}}{sen(\theta _{b}+\theta _{i}})=-1 \\ \Rightarrow E_{r}=-E_{i} = -E_{0} cos (k_{x}) = -2 cos k_{x}$

c)Décrire la polarisation de l'onde reflétée:
Comme r\perp est inféreur à 0, Ez change de signe, Ex lui, conserve sa direction.

Merci de votre aide!

Jorg

Posté par re : champ électrique d'une onde dans un milieu 24-10-16 à 21:58

Bonsoir
D'accord avec toi pour la réflexion totale de l'onde si l'angle d'incidence vaut 60°.
Je n'ai pas l'énoncé exact de l'exercice... Le champ électrique incident à une composante appartenant au plan d'incidence et une autre orthogonale, chacune d'amplitude voisine de 1,4N/C. Je me demande s'il ne faut pas écrire les expressions de ces composantes du champ électrique après la réflexion totale. Ne faut-il pas aussi étudier les composantes du vecteur B avant et après la réflexion totale ?

Posté par re : champ électrique d'une onde dans un milieu 24-10-16 à 22:30

Bonsoir, merci pour votre réponse!

Dans le cours, il est écrit qu'une onde peut avoir une polarisation parallèle, perpendiculaire, ou les deux par rapport au plan d'incidence. Comme il est ici précisé que l'onde est polarisée linéairement et perpendiculairement à ce plan, je ne comprends pas comment il peut quand même avoir une composante parallèle.
Par ailleurs, comment obtient-on une amplitude voisine de 1,4 N/C?

Pour ce qui est de l'énoncé, c'est tout ce que j'ai, je peux le réécrire plus clairement:
Une onde monochromatique de 550 nm incide sur une surface eau/air avec un angle de 60°. Sa polarisation est linéaire formant un angle de 45° du plan d'incidence et son amplitude Eo=2 N/C
a) obtenir le vecteur d'onde transmise $k_{tC}$ .
b) Écrire l'expression du champ électrique de l'onde réfléchie exprimée en composantes parallèles et perpendiculaires.
c)Décrire la polarisation de l'onde reflétée.

Je vais essayer de décrire les composantes plus précisément.

Posté par re : champ électrique d'une onde dans un milieu 25-10-16 à 23:15

Bonsoir
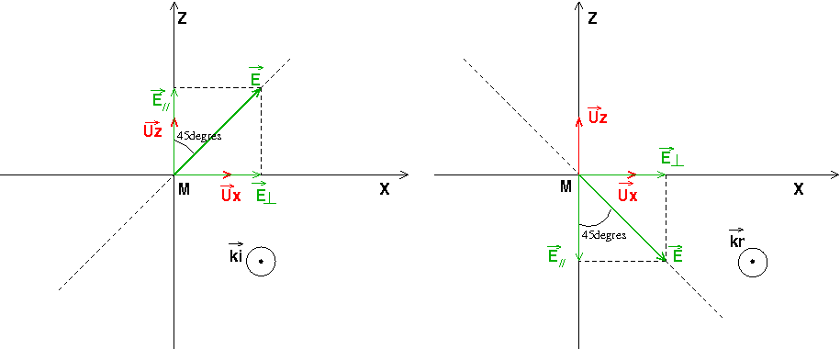
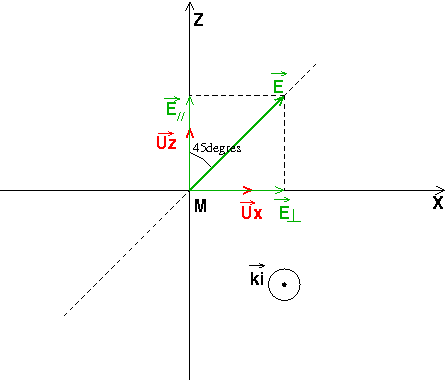
Voici un schéma qui pourras t'aider mais attention : les noms des axes que j'ai choisis ne correspondent peut-être pas à ton problème : je te laisse adapter ! J'imagine la propagation de l'onde plane dans l'eau, la direction de propagation est caractérisée par le vecteur $\overrightarrow{k_{i}}$ perpendiculaire au plan de figure. Le plan d'incidence est le plan $\left(M,\overrightarrow{k_{i}},\overrightarrow{U_{z}}\right)$ . La direction de polarisation rectiligne est la ligne noire en pointillé incliné de 45° par rapport au plan d'incidence. Le représentant du vecteur champ a constamment la direction de cette ligne en pointillé. On voit bien qu'à chaque instant, le vecteur champ E est la somme de deux vecteurs, le vecteur $\overrightarrow{E_{//}} \\$ et le vecteur $\overrightarrow{E_{\perp}}$ . L'amplitude de chaque composante est le produit de l'amplitude du champ résultant par $\frac{\sqrt{2}}{2}$

Je pense qu'il faut étudier le comportement de chaque vecteur champ lors de la réflexion totale.

$champ électrique d\'une onde dans un milieu$

Posté par re : champ électrique d'une onde dans un milieu 26-10-16 à 00:49

Bonsoir!

En effet, c'est beaucoup plus clair avec ce schéma; j'ai trouvé r perp = -1 et r par = 1.
J'en ai déduit que:
$E_{r} = E\perp _{r} + E\parallel _{r} = E\parallel _{i} - E\perp _{i} = E_{i}^{z} - E_{i}^{y} = E_{0} cos (60) - sen (60)$
( Je crois que mes axes z et y sont inversés par rapport au schéma)

Par ailleurs, r parallèle étant supérieur à 0, Ex change de direction.

Je ne suis pas sûre pour ma composante perpendiculaire: j'ai cru comprendre dans un livre que les composantes perpendiculaires et parallèles faisaient toujours 1 pour une réflexions totale. Ai-je bien compris?
Merci!

Posté par re : champ électrique d'une onde dans un milieu 26-10-16 à 22:39

Bonsoir
Je garde les notations de mon message précédent. Le vecteur champ électrique de l'onde incidente peut s'écrire sous la forme :

$\overrightarrow{E}=E_{0}\cdot\frac{\sqrt{2}}{2}\cdot\left(\overrightarrow{U_{x}}+\overrightarrow{U_{z}}\right)\cdot\cos\left(\omega t-\overrightarrow{k_{i}}\cdot\overrightarrow{OM}+\varphi\right) \\$

Je note $\vec{k_r}$ le vecteur d'onde associée à l'onde plane réfléchie ; c'est le vecteur symétrique du vecteur d'onde incident $\vec{k_i}$ par rapport à la normale au dioptre. Pour une réflexion totale : $r_{//}=-1$ et $r_{\perp}=1$ : les deux composantes conservent leur amplitude mais la composante appartenant au plan d'incidence subit un déphasage de rad. L'expression du vecteur champ correspondant à l'onde réfléchie peut s'écrire :

$\overrightarrow{E}=E_{0}\cdot\frac{\sqrt{2}}{2}\cdot\left(\overrightarrow{U_{x}}-\overrightarrow{U_{z}}\right)\cdot\cos\left(\omega t-\overrightarrow{k_{r}}\cdot\overrightarrow{OM}+\varphi\right)$
avec : E_o=2N/C.
l'onde réfléchie est encore polarisée rectilignement mais la direction de polarisation a tourné de 90° par rapport à la direction de polarisation de l'onde incidente.

$champ électrique d\'une onde dans un milieu$